CMR: 3+32+33+....+31997+31998 chia hết cho 26
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
G
1
30 tháng 12 2022
Số các số hạng là: 101 – 0 + 1 = 102 số.
Ta nhận thấy:
1 + 3 + 32 = 1 + 3 + 9 = 13;
33 + 34 + 35 = 33(1 + 3 + 32) = 33.13;
…
Mà 102 có tổng các chữ số là 1 + 0 + 2 = 3 chia hết cho 3 nên 102 chia hết cho 3, nghĩa là:
A = (1 + 3 + 32) + (33 + 34 + 35) + … + (399 + 3100 + 3101)
= (1 + 3 + 32) + 33(1 + 3 + 32) + … + 399(1 + 3 + 32)
= 13 + 33.13 + … + 399.13
= 13.(1 + 33 + … + 399) chia hết cho 13.
Vậy A chia hết cho 13.
25 tháng 8 2021
b: Gọi số bị trừ là x
Số trừ là x-98
Theo đề, ta có: \(x\left(x-98\right)=1998\)
\(\Leftrightarrow x^2-98x-1998=0\)
mà x nguyên
nên \(x\notin\varnothing\)
ND
1
11 tháng 11 2021
A =3+32+33+...+3119
A=(3+32)+(33+34)+...(3118+3119)
A=3.(1+3)+33.(1+3)+...+3118.(1+3)
A=3.4+33.4+...+3118.4
A=4.(3+33+...+3118)\(⋮\)4
=>A\(⋮\)4
A=3+32+33+...+3119
A=(3+32+33)+...+(3117+3118+3119)
A=3.(1+3+9)+...+3117.(1+3+9)
A=3.13+...+3117.13
A=13.(3+...+3117)\(⋮\)13
vì A\(⋮\)4
và A\(⋮\)13
=>A\(⋮\)4.13
=>A\(⋮\)52
vậy A\(⋮\)4 và A\(⋮\)52
MV
0
NS
0
9 tháng 7 2021
Ta có: `B = 1 + 3 + 3^2 + ... + 3^1991`
`= (1 + 3 + 3^2) + (3^3 + 3^4 + 3^5) + ... + (3^1989 + 3^1990 + 3^1992)`
`= 13 + 3^3 (1 + 3 + 3^2) + ... + 3^1989 (1 + 3 + 3^2)`
`= 13 + 3^3 . 13 + ... + 3^1989 . 13`
`= 13 (1 + 3^3 + ... + 3^1989)`
Vì \(13\left(1+3^3+...+3^{1989}\right)⋮13\) nên \(B⋮13\)
`B = 1 + 3 + 3^2 + ... + 3^1991`
= (1 + 3^4) + (3 + 3^5) + ... + (3^1987 + 3^1991)`
`= 82 + 3 (1 + 3^4) + ... + 3^1987 (1 + 3^4)`
`= 82 + 3 . 82 + ... + 3^1987 . 82`
`= 82 (1 + 3 + ... + 3^1987)`
Vì \(82\left(1+3+...+3^{1987}\right)⋮41\) nên \(B⋮41\)
`C = 3 + 3^2 + 3^3 + ... + 3^1000`
\(=\left(3+3^2+3^3+3^4\right)+\left(3^5+3^6+3^7+3^8\right)+...+\left(3^{997}+3^{998}+3^{999}+3^{1000}\right)\)
`= 120 + 3^4 (3 + 3^2 + 3^3 + 3^4) + ... + 3^996 (3 + 3^2 + 3^3 + 3^4)`
`= 120 + 3^4 . 120 + ... + 3^996 . 120`
`= 120 (1 + 3^4 + ... + 3^996)`
Vì \(120\left(1+3^4+...+3^{996}\right)⋮120\) nên \(C⋮120\)
9 tháng 7 2021
Ta có: \(C=3+3^2+3^3+...+3^{1000}\)
\(=\left(3+3^2+3^3+3^4\right)+\left(3^5+3^6+3^7+3^8\right)+...+\left(3^{997}+3^{998}+3^{999}+3^{1000}\right)\)
\(=120\left(1+3^5+...+3^{997}\right)⋮120\)(đpcm)
AH
Akai Haruma
Giáo viên
13 tháng 10 2023
Lời giải:
$S=3^1.3^2.3^3....3^{1998}=3^{1+2+3+...+1998}=3^{1997001}$
Ta thấy các ước của $S$ có dạng $3^m$ với $0\leq m\leq 1997001$ với $m$ là số tự nhiên.
Do đó $S\not\vdots 26$
KV
23 tháng 12 2023
A = 8⁸ + 2²⁰
= (2³)⁸ + 2²⁰
= 2²⁴ + 2²⁰
= 2²⁰.(2⁴ + 1)
= 2²⁰.17 ⋮ 17
Vậy A ⋮ 17
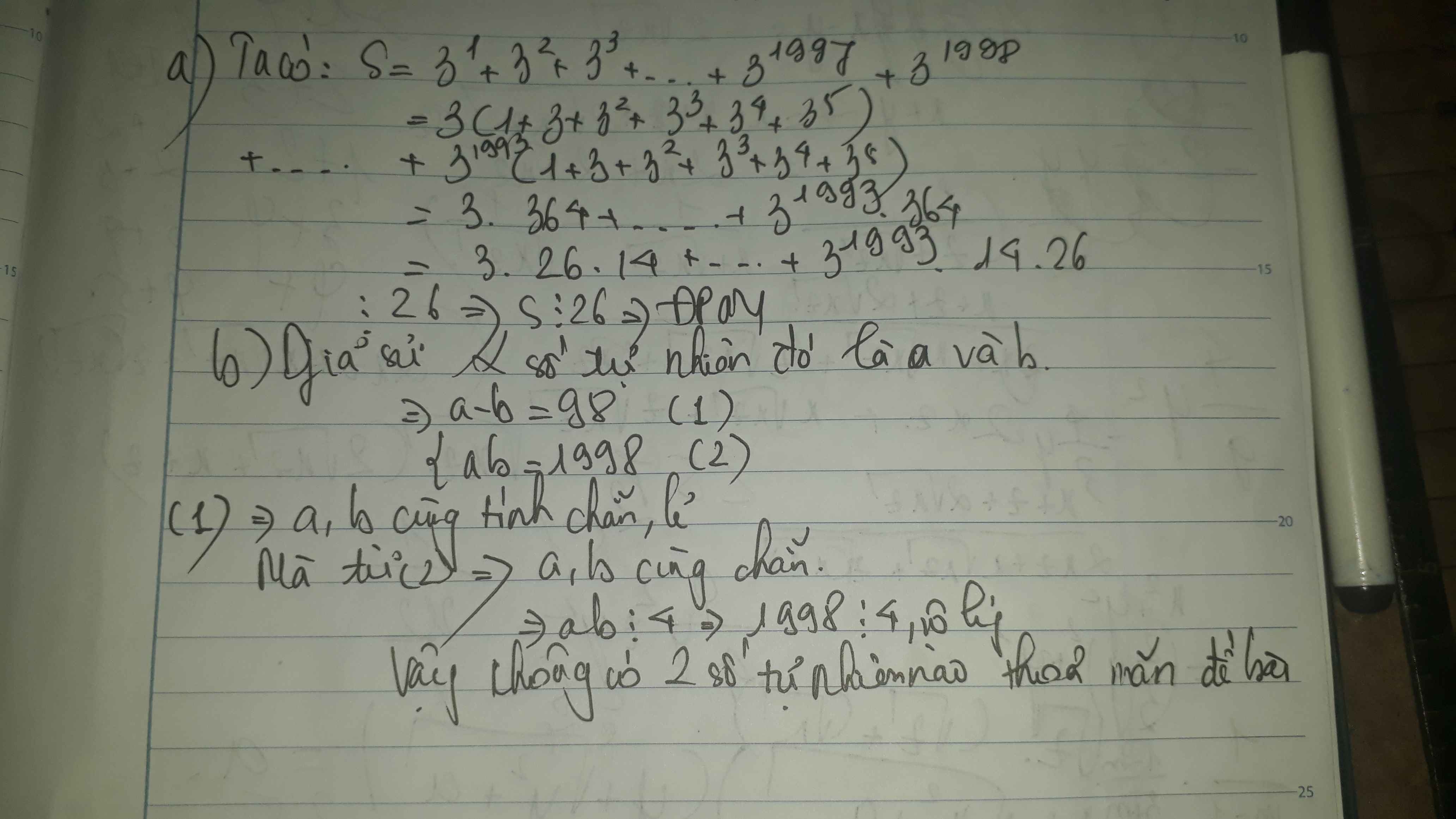
Nhóm các nhóm 2,3,4... số vào nhé bạn