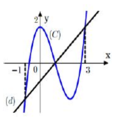
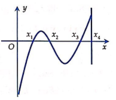
Cho hàm số bậc 4 y = f(x) có đồ thị như hình vẽ bên. Biết hàm số y = f(x) đạt cực trị tại các điểm x1,x2,x3 thỏa mãn x3 = x1+2, f(x1) + f(x3) +\(\dfrac{2}{3}\)f(x2) = 0 và (C) nhận đường thẳng x = x2 làm trục đối xứng. Gọi S1,S2,S3,S4 là diện tích của các miền hình phẳng được đánh dấu như hình bên. Tỉ số \(\dfrac{S_1+S_2}{S_3+S_4}\) gần với kết quả nào nhất :
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

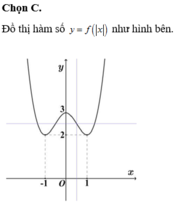
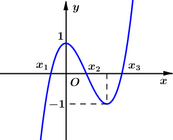
Đồ thị hàm số có điểm uốn là trung điểm của 2 đường cực trị I 1 2 ; 5 2
Số nghiệm của phương trình f(|x|)=m là số giao điểm của đồ thị hàm số y=f(|x|) và đường thẳng y=m. Để phương trình có 4 nghiệm thỏa mãn điều kiện đề bài thì 5 2 ≤ m < 3

Đáp án A
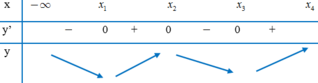
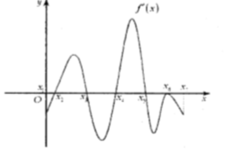
Dựa vào đồ thị hàm số y = f ' x , ta có nhận xét:
Hàm số y = f ' x đổi dấu từ – sang + khi qua x = x 1 .
Hàm số y = f ' x đổi dấu từ + sang – khi qua x = x 2 .
Hàm số y = f ' x đổi dấu từ – sang + khi qua x = x 3 .
Từ đó ta có bảng biến thiên của hàm số y = f x trên đoạn 0 ; x 4 như sau:
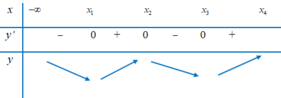
Sử dụng bảng biến thiên ta tìm được max 0 ; x 4 [ f x = max f 0 , f x 2 , f x 4 min 0 ; x 4 f x = min f x 1 , f x 3 .
Quan sát đồ thị, dùng phương pháp tích phân để tính diện tích, ta có:
∫ x 1 x 2 f ' x d x < ∫ x 2 x 3 0 − f ' x d x ⇒ f x 3 < f x 1 ⇒ min 0 ; x 4 f x = f x 3
Tương tự, ta có
∫ 0 x 1 0 − f ' x d x > ∫ x 1 x 2 f ' x d x ⇒ f 0 > f x 2 ∫ x 2 x 3 0 − f ' x d x > ∫ x 3 x 4 f ' x d x ⇒ f x 2 > f x 4
⇒ f 0 > f x 2 > f x 4 ⇒ max 0 ; x 4 f x = f x 3
Vậy max 0 ; x 4 f x = f 0 ; min 0 ; x 4 f x = f x 3

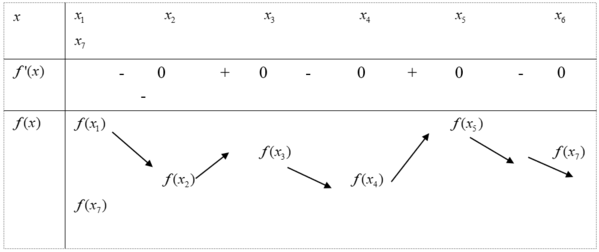
Do \(f\left(x\right)=ax^4+bx^3+cx^2+dx+e\) có 4 nghiệm pb \(x_1;x_2;x_3;x_4\)
\(\Rightarrow f\left(x\right)=a\left(x-x_1\right)\left(x-x_2\right)\left(x-x_3\right)\left(x-x_4\right)\)
Ta có:
\(f'\left(x\right)=a\left[\left(x-x_1\right)\left(x-x_2\right)\left(x-x_3\right)+\left(x-x_2\right)\left(x-x_3\right)\left(x-x_4\right)+\left(x-x_1\right)\left(x-x_3\right)\left(x-x_4\right)+\left(x-x_1\right)\left(x-x_2\right)\left(x-x_4\right)\right]\)
\(\Rightarrow\left\{{}\begin{matrix}f'\left(x_1\right)=a\left(x_1-x_2\right)\left(x_1-x_3\right)\left(x_1-x_4\right)\\f'\left(x_2\right)=a\left(x_2-x_1\right)\left(x_2-x_3\right)\left(x_2-x_4\right)\\f'\left(x_3\right)=a\left(x_3-x_1\right)\left(x_3-x_2\right)\left(x_3-x_4\right)\\f'\left(x_4\right)=a\left(x_4-x_1\right)\left(x_4-x_2\right)\left(x_4-x_3\right)\end{matrix}\right.\)
Mà tiếp tuyến tại A và B vuông góc \(\Leftrightarrow f'\left(x_1\right).f'\left(x_2\right)=-1\) (1)
Do \(x_1;x_2;x_3;x_4\) lập thành 1 CSC, giả sử công sai của CSC là \(d\)
\(\Rightarrow\left\{{}\begin{matrix}x_2=x_1+d\\x_3=x_1+2d\\x_4=x_1+3d\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}f'\left(x_1\right)=a.\left(-d\right).\left(-2d\right).\left(-3d\right)=-6ad^3\\f'\left(x_2\right)=a.d.\left(-d\right).\left(-2d\right)=2ad^3\\f'\left(x_3\right)=a.2d.d.\left(-d\right)=-2ad^3\\f'\left(x_4\right)=a.3d.2d.d=6ad^3\end{matrix}\right.\)
Thế vào (1): \(-12a^2d^6=-1\Leftrightarrow12a^2d^6=1\)
\(\Rightarrow f'\left(x_3\right)+f'\left(x_4\right)=4ad^3\)
\(\Rightarrow S=\left(4ad^3\right)^{2020}=\left(16a^2d^6\right)^{1010}=\left(\dfrac{4}{3}.12a^2d^6\right)^{1010}=\left(\dfrac{4}{3}\right)^{1010}\)
Bài gì mà dễ sợ :(
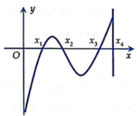


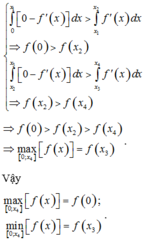

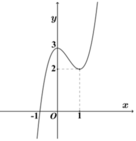

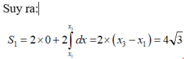
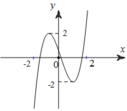

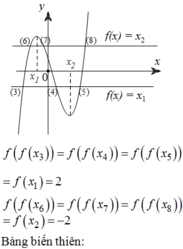
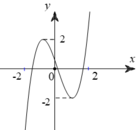

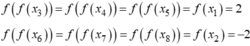

Có thể nghịch suy để chọn hàm làm trắc nghiệm
Do \(x_2=\dfrac{x_3-x_1}{2}=1\) nên hàm có dạng: \(y=a\left(x-1\right)^4-b\left(x-1\right)^2+c\) với a;b;c dương
\(y'=0\Rightarrow\left[{}\begin{matrix}x-1=0\\\left(x-1\right)^2=\dfrac{b}{2a}\end{matrix}\right.\) \(\Rightarrow x_1;x_3\) thỏa mãn \(\left(x-1\right)^2=\dfrac{b}{2a}\) và \(f\left(x_2\right)=c\)
\(f\left(x_1\right)+f\left(x_3\right)+\dfrac{2}{3}f\left(x_2\right)=0\Leftrightarrow2f\left(x_1\right)+\dfrac{2}{3}f\left(x_2\right)=0\)
\(\Leftrightarrow a.\left(\dfrac{b}{2a}\right)^2-b\left(\dfrac{b}{2a}\right)+c+\dfrac{c}{3}=0\Rightarrow-\dfrac{b^2}{4a}+\dfrac{4c}{3}=0\)
Tới đây chọn \(a=3;c=1;b=4\) được hàm \(f\left(x\right)=3\left(x-1\right)^4-4\left(x-1\right)^2+1\)
Dễ dàng tính ra \(x_3=1+\sqrt{\dfrac{2}{3}}\) ; \(x_0=1+\sqrt{\dfrac{1}{3}}\) (với \(x_0\) là giao bên phải của đồ thị và trục hoành); \(f\left(x_1\right)=f\left(x_3\right)=-\dfrac{1}{3}\)
\(S_1+S_2=\int\limits^{x_0}_1f\left(x\right)dx-\int\limits^{x_3}_{x_0}f\left(x\right)dx\approx0,41\)
\(\dfrac{S_1+S_2}{S_3+S_4}=\dfrac{0,41}{\left(1+\dfrac{1}{3}\right)\left(x_3-1\right)-0,41}\approx0,6\)