Một chiếc cốc có dạng hình trụ, chứa đầy nước. Hỏi nếu bỏ vào cốc 5 viên đá dạng hình lập phương có cạnh 2 cm thì lượng nước trào ra ngoài là bao nhiêu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Thể tích 10 viên đất là:
10*2^3=80cm3
Diện tích đáy cốc là: pi*R^2=200,96cm2
Mực nước dâng lên:
80/200,96=0,4(cm)

cho mình hỏi chỗ v1 sao lại là 5 . \(\dfrac{4}{3}\pi R^3\) vậy ạ

Đáp án B
Phương pháp:
Tính thể tích mỗi viên bi hình cầu: V = 4 3 π R 3 ⇒ 5 viên có thể tích
Tính thể tích lượng nước ban đầu (cột nước hình trụ): V 2 = V n = π R 2 h .
Tính tổng thể tích cả bi và nước lúc sau V = V 1 + V 2 , từ đó suy ra chiều cao cột nước lúc sau và khoảng cách từ mặt nước đến miệng cốc.
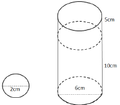
Cách giải:
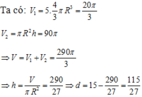
Chú ý khi giải:
Các em có thể sẽ quên không tính thể tích của 5 viên bi, hoặc nhầm lẫn đường kính 6cm thành bán kinh 6cm dẫn đến các thể tích bị sai.

Diện tích đáy của cái cốc là: \(\pi.4^2=16\pi\left(cm^2\right)\)
Thể tích của \(3\)viên bi là: \(3.\frac{4}{3}\pi.1^3=4\pi\left(cm^3\right)\)
Mực nước cao lên số cen-ti-mét là: \(\frac{4\pi}{16\pi}=0,25\left(cm\right)\)
Nước dâng cao cách miệng cốc: \(12-8-0,25=3,75\left(cm\right)\)


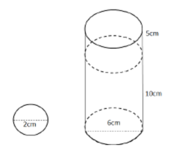




Thể tích của một viên đá là :\(2.2.2 = 8\left( {c{m^3}} \right)\)
Tổng thể tích của 5 viên đá là :\(8.5 = 40\left( {c{m^3}} \right)\)
Thể tích của 5 viên đá sẽ bằng thể tích lượng nước dâng lên sau khi cho đá vào
Do đó, lượng nước tràn ra sẽ là \(40c{m^3}\) nước.