Hỏi có tam giác nào với độ dài ba cạnh là 2,5 cm; 3,4 cm và 6 cm không? Vì sao?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Theo bất đẳng thức tam giác:
a) Vì 2 + 3 = 5 nên bộ ba đoạn thẳng có độ dài 2 cm, 3 cm, 5 cm không thể là độ dài ba cạnh của một tam giác
b) Vì 3+4 > 6 nên bộ ba đoạn thẳng có độ dài 3 cm, 4 cm, 6 cm có thể là độ dài ba cạnh của một tam giác

* Cách vẽ: + Vẽ độ dài cạnh AB = 6cm.
+ Dùng compa, vẽ cung tròn tâm A bán kính 3 cm, cung tròn tâm B bán kính 4cm. Hai cung tròn này cắt nhau tại C.
Ta được tam giác ABC cần vẽ.
c) Vì 2+4 > 5 nên bộ ba đoạn thẳng có độ dài 2 cm, 4 cm, 5 cm có thể là độ dài ba cạnh của một tam giác
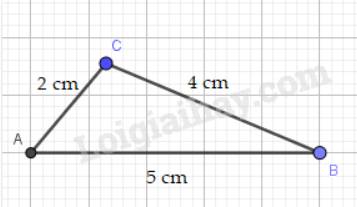
* Cách vẽ: + Vẽ độ dài cạnh AB = 5cm.
+ Dùng compa, vẽ cung tròn tâm A bán kính 2 cm, cung tròn tâm B bán kính 4cm. Hai cung tròn này cắt nhau tại C.
Ta được tam giác ABC cần vẽ.

a) Vì 5+4 > 6 nên ba độ dài 5 cm, 4 cm, 6 cm có thể là độ dài ba cạnh của một tam giác.

b) Vì 3 + 6 = 9 < 10 nên ba độ dài 3 cm, 6 cm, 10 cm không thể là độ dài ba cạnh của một tam giác

ΔABC đồng dạng với ΔMNP
=>\(\dfrac{AB}{MN}=\dfrac{BC}{NP}=\dfrac{AC}{MP}\)
ΔABC đồng dạng với ΔMNP
=>Độ dài cạnh nhỏ nhất của ΔMNP sẽ là độ dài tương ứng với cạnh nhỏ nhất của ΔABC
mà cạnh nhỏ nhất của ΔABC là AB và cạnh tương ứng của AB trong ΔMNP là MN
nên MN=2,5cm
=>\(\dfrac{5}{2,5}=\dfrac{12}{MP}=\dfrac{13}{NP}\)
=>\(\dfrac{12}{MP}=\dfrac{13}{NP}=2\)
=>MP=12/2=6(cm); NP=13/2=6,5(cm)

Giải:
Gọi 3 cạnh của tam giác ABC lần lượt là a, b, c ( a > b > c > 0 )
Ta có: \(\frac{a}{5}=\frac{b}{4}=\frac{c}{3}\) và a - c = 10
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{5}=\frac{b}{4}=\frac{c}{3}=\frac{a-c}{5-3}=\frac{10}{2}=5\)
+) \(\frac{a}{5}=5\Rightarrow a=25\)
+) \(\frac{b}{4}=5\Rightarrow b=20\)
+) \(\frac{c}{3}=5\Rightarrow c=15\)
Vậy 3 cạnh của tam giác lần lượt là 15 cm, 20 cm và 25 cm
Gọi độ dài các cạnh của tam giác lần lượt là a , b , c (theo thứ tự nhỏ đến lớn)
Theo đề bài , ta có :
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\) và c + 10 = a + b
Áp dụng tính chất dãy tỉ số bằng nhau , ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{a+b}{3+4}=\frac{c+10}{7}\)
=> \(\frac{c+10}{7}=\frac{c}{5}\)
=> 5(c + 10) = 7c
=> 5c + 50 = 7c
=> 50 = 2c
=> c = 25
=> a + b = 25 + 10 = 35
Áp dụng tính chất dãy tỉ số , ta có :
\(\frac{a}{3}=\frac{b}{4}=\frac{a+b}{3+4}=\frac{35}{7}=5\)
=> a = 3.5 = 15
b = 4.5 = 20

Gọi 3 cạnh của tam giác lần lượt là \(a, b, c ( cm) (a,b,c > 0)\)
Theo đề bài 3 cạnh của tam giác tỉ lệ với 3, 4, 5 nên ta có tỉ số \(a : b : c = 3 : 4 : 5.\)
Và chu vi tam giác là 60cm nên ta có:\( a + b + c = 60.\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\( \Rightarrow \dfrac{a}{3} = \dfrac{b}{4} = \dfrac{c}{5} = \dfrac{{a + b + c}}{{12}} = \dfrac{{60}}{{12}} = 5\)
\( \Rightarrow a = 3.5=15 ; b = 4.5=20 ; c = 5.5=25.\)
Vậy 3 cạnh của tam giác có độ dài là \(15cm, 20cm, 25cm.\)

Gọi độ dài cạnh thứ ba của tam giác là x cm (x > 0)
Áp dụng bất đẳng thức trong tam giác ta có: 10 – 2 < x < 10 + 2
Hay 8 < x < 12
Trong bốn đáp án A, B, C, D thì đáp án D thỏa mãn vì 8 < 9 < 12
Vậy độ dài cạnh thứ ba là 9 cm.
Chọn đáp án D
Ta có: 2,5 + 3,4 = 5,9 cm < 6 cm nên không có tam giác nào với độ dài ba cạnh là 2,5 cm; 3,4 cm và 6 cm.