Cho tam giác cân ABC, AB = AC. Lấy điểm M tùy ý nằm giữa B và C. ( H. 9.12)
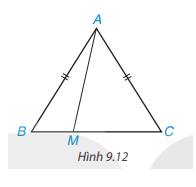
a) Khi M thay đổi thì độ dài AM thay đổi. Xác định vị trí của điểm M để độ dài AM nhỏ nhất.
b) Chứng minh rằng với mọi điểm M thì AM < AB
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

dễ thấy tứ giác ADME là hình chữ nhật do có 3 góc vuông
nên chu vi ADME=2(AE+EM)
mà do ABC vuông cân nên góc ECM =45 độ nên MEC vuông cân tại E nên EM=EC
nên chu vi ADME=2(AE+EM)=2(AE+EC)=2AC là không đổi
b.DE=AM nhỏ nhaasrt khi M là hình chiếu của A lên BC

a: Ta có: D đối xứng với M qua AB
nên AB là đường trung trực của MD
Suy ra: AM=AD
Xét ΔAMD có AM=AD
nên ΔAMD cân tại A
mà AB là đường trung trực ứng với cạnh đáy MD
nên AB là tia phân giác của \(\widehat{MAD}\)
Ta có: D và N đối xứng nhau qua AC
nên AC là đường trung trực của ND
Suy ra: AN=AD
Xét ΔAND có AN=AD
nên ΔAND cân tại A
mà AC là đường trung trực ứng với cạnh đáy DN
nên AC là tia phân giác của \(\widehat{DAN}\)
Ta có: \(\widehat{MAN}=\widehat{MAD}+\widehat{NAD}\)
\(=2\cdot\left(\widehat{BAD}+\widehat{CAD}\right)\)
\(=2\cdot\widehat{BAC}\)

a) Ta có: D đối xứng với M qua AB
=> AB là đường trung trực của MD
Xét tam giác AMD có:
AB là đường trung trực của MD(cmt)
=> Tam giác AMD cân tại A
=> AB là tia phân giác \(\widehat{MAD}\Rightarrow\widehat{MAD}=2\widehat{BAD}\)
CMTT => AC là tia phân giác \(\widehat{DAN}\Rightarrow\widehat{DAN}=2\widehat{DAC}\)
Ta có: \(\widehat{MAN}=\widehat{MAD}+\widehat{DAN}=2\left(\widehat{BAD}+\widehat{DAC}\right)=2\widehat{BAC}\)
=> \(\widehat{MAN}\) có số đo không đổi
Kẻ AH BC.
a) Trong các đường xiên và đường vuông góc kẻ từ A điểm nằm ngoài đường thẳng BC đến đường thẳng BC thì đường vuông góc là đường ngắn nhất nên AM ngắn nhất khi M trùng H hay M là chân đường vuông góc kẻ từ A đến BC.
b) Cách 1:
+) Khi M trùng H thì AH < AB ( đường vuông góc luôn nhỏ hơn đường xiên)
+) Khi M nằm giữa B và H
Góc AMB là góc ngoài tại đỉnh M của tam giác AHM nên \(\widehat{AMB}>\widehat{AHM}= 90^0\) nên \(\widehat{AMB}\) là góc tù nên là góc lớn nhất trong tam giác ABM.
Trong tam giác ABM, cạnh AB đối diện với góc lớn nhất nên cạnh AB lớn nhất (định lí). Do đó AM < AB.
+) Khi M nằm giữa C và H
Góc AMC là góc ngoài tại đỉnh M của tam giác AHM nên \(\widehat{AMC}>\widehat{AHM}= 90^0\) nên \(\widehat{AMC}\) là góc tù nên là góc lớn nhất trong tam giác ACM
Trong tam giác ACM, cạnh AC đối diện với góc lớn nhất nên cạnh AC lớn nhất (định lí). Do đó AM < AC.
Mà AB = AC (gt)
\(\Rightarrow \) AM < AB
Vậy AM < AB
Cách 2:
Theo thử thách nhỏ trang 64, khi M thay đổi trên BC, M càng xa H thì AM càng lớn lên. Tuy nhiên, M nằm giữa B và C nên AM không vượt quá AB. Như vậy, AM < AB