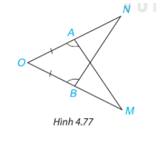
Trong Hình 4.77, có AO = BO,\(\widehat {OAM} = \widehat {OBN}\). Chứng minh rằng AM = BN.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Xét \(\Delta MNA\) và \(\Delta MNB \) có:
AM=BM (gt)
AN=BN (gt)
MN chung
=>\(\Delta MNA = \Delta MNB\) (c.c.c)
=>\(\widehat {MAN} = \widehat {MBN}\) (2 góc tương ứng)
QT
1
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
Ta có: \(\widehat A = \widehat B\)
Mà 2 góc này ở vị trí so le trong nên AM // BN
\(\Rightarrow \widehat M = \widehat N\)(2 góc so le trong).
Xét hai tam giác AOM và BON có: \(\widehat A = \widehat B\), AM = BN, \(\widehat M = \widehat N\).
Vậy \(\Delta AOM = \Delta BON\) (g.c.g)
Do đó OA = OB, OM = ON. (2 cạnh tương ứng).
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Xét \(\Delta ANB \) và \(\Delta BMA\) có:
AN=BM (gt)
\(\widehat {BAN} = \widehat {ABM}\) (gt)
AB chung
=>\(\Delta ANB = \Delta BMA\)(c.g.c)
=> \(\widehat{ABN} = \widehat{BAM}\) (2 góc tương ứng)
MH
28 tháng 9 2023
\(Am//Ox\Rightarrow\widehat{xOy}=\widehat{mAy}=a\)
\(\Rightarrow\widehat{OAm}=180^o-\widehat{mAy}=180^o-a\)
28 tháng 9 2023
`#3107`
Ta có:
`\text {AM // Ox}`
`=>` \(\widehat{\text{xOA}}=\widehat{\text{A}_1}\) (2 góc đồng vị)
Mà \(\widehat{\text{A}_1}\) và \(\widehat{\text{OAm}}\) là 2 góc kề bù
`=>`\(\widehat{\text{A}_1}+\widehat{\text{OAm}}=180^0\)
`=>`\(\widehat{\text{xOA}}+\widehat{\text{OAm}}=180^0\)
`=>`\(a+\widehat{\text{ }\text{OAm}}=180^0\)
`=>`\(\widehat{\text{OAm}}=180^0-a\)
Vậy, để `\text {AM // Ox}` thì cần thỏa mãn \(\widehat{\text{OAm}}=180^0-a.\)
Xét 2 tam giác OAM và OBN có:
\(\widehat {OAM} = \widehat {OBN}\) (gt)
AO=BO (gt)
\(\widehat{O}\) chung
=>\(\Delta OAM = \Delta OBN\)(g.c.g)
=>AM=BN (2 cạnh tương ứng)