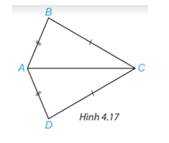
Cho hình 4.17, biết AB=AD, BC=DC. Chứng minh rằng \(\Delta ABC = \Delta ADC\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A B C D
a, Xét \(\Delta ADB;\Delta ADC\) có :
\(\left\{{}\begin{matrix}AB=AC\\DB=DC\\ADchung\end{matrix}\right.\)
\(\Leftrightarrow\Delta ADB=\Delta ADC\left(c-c-c\right)\)
b, \(\Delta ADB=\Delta ADC\left(cmt\right)\)
\(\Leftrightarrow\widehat{BDA}=\widehat{ADC}\)
Lại có :
\(\widehat{BDA}+\widehat{ADC}=180^0\left(kềbuf\right)\)
\(\Leftrightarrow\widehat{BDA}+\widehat{ADC}=\dfrac{180^0}{2}=90^0\)
\(\Leftrightarrow AD\perp BC\)

Tự kẽ hình nha :
a) Xét tam giác AHB và tam giác ABC có :
\(\widehat{A}\) = \(\widehat{H}\) = 900
\(\widehat{B}\) = góc chung
=.tam giác AHB ~ tam giác CAB ( g.g)
b) ADĐL pitago và tam giác vuông ABC , có :
AB2 + AC2 = BC2
122 + 162 = BC2
BC2 = 400
=> BC = 20 cm
Vì tam giác AHB ~ tam giác CAB ( câu a) , ta có :
\(\dfrac{AH}{AC}\)= \(\dfrac{AB}{BC}\)
=.> \(\dfrac{AH}{16}\)= \(\dfrac{12}{20}\)
=> AH = 9,6 cm
c)
Thay : \(\dfrac{EA}{EB}\)= \(\dfrac{DB}{DC}\)=\(\dfrac{FC}{FA}\)
Thành : \(\dfrac{AD}{DB}\)=\(\dfrac{DB}{BC}\)= \(\dfrac{BC}{AD}\)
Mà : \(\dfrac{AD}{DB}\)=\(\dfrac{DB}{BC}\)=\(\dfrac{BC}{AD}\)= 1
=> \(\dfrac{EA}{EB}\)=\(\dfrac{DB}{DC}\)=\(\dfrac{FC}{FA}\)= 1

a: Xét ΔABD và ΔACD có
AB=AC
BD=CD
AD chung
Do đó: ΔABD=ΔACD
=>\(\widehat{BAD}=\widehat{CAD}\)
=>AD là phân giác của góc BAC
b: Sửa đề: DM\(\perp\)AB tại M. Chứng minh AC\(\perp\)DN
Xét ΔAMD và ΔAND có
AM=AN
\(\widehat{MAD}=\widehat{NAD}\)
AD chung
Do đó: ΔAMD=ΔAND
=>\(\widehat{AMD}=\widehat{AND}\)
mà \(\widehat{AMD}=90^0\)
nên \(\widehat{AND}=90^0\)
=>DN\(\perp\)AC
c: Xét ΔKCD và ΔKNE có
KC=KN
\(\widehat{CKD}=\widehat{NKE}\)(hai góc đối đỉnh)
KD=KE
Do đó: ΔKCD=ΔKNE
d: Xét ΔABC có \(\dfrac{AM}{AB}=\dfrac{AN}{AC}\)
nên MN//BC
Ta có: ΔKCD=ΔKNE
=>\(\widehat{KCD}=\widehat{KNE}\)
mà hai góc này là hai góc ở vị trí so le trong
nên NE//DC
=>NE//BC
ta có: NE//BC
MN//BC
NE,MN có điểm chung là N
Do đó: M,N,E thẳng hàng

b
Δ ABD ⊥ tại D có DE là đường cao.
=> \(AD^2=AE.AB\) (hệ thức lượng) (1)
Δ ADC ⊥ tại C có DC là đường cao.
=> \(AD^2=AF.AC\) (hệ thức lượng) (2)
Từ (1), (2) suy ra: \(AE.AB=AF.AC\left(=AD^2\right)\)
Xét Δ AEF và Δ ACB có:
\(\widehat{EAF}=\widehat{CAB}\) (góc chung)
\(\dfrac{AF}{AE}=\dfrac{AB}{AC}\left(cmt\right)\)
=> Δ AEF đồng dạng Δ ACB (c.g.c)

a: Xét ΔABC và ΔAED có
AB/AE=AC/AD
góc BAE chung
Do đó: ΔABC\(\sim\)ΔAED
b: Xét ΔFBD và ΔFEC có
\(\widehat{FDB}=\widehat{FCE}\left(=\widehat{ADE}\right)\)
góc BFD chung
Do đó: ΔFBD\(\sim\)ΔFEC
c: BD=AB-AD=4,8-3,2=1,6(cm)
EC=AC-AE=6,4-2,4=4(cm)
Ta có: ΔADE\(\sim\)ΔACB
nên DE/CB=AD/AC=3,2/6,4=1/2
=>DE=1,8(cm)

a: Xét ΔABC và ΔAED có
AB/AE=AC/AD
góc BAE chung
Do đó: ΔABC\(\sim\)ΔAED
b: Xét ΔFBD và ΔFEC có
\(\widehat{FDB}=\widehat{FCE}\left(=\widehat{ADE}\right)\)
góc BFD chung
Do đó: ΔFBD\(\sim\)ΔFEC
c: BD=AB-AD=4,8-3,2=1,6(cm)
EC=AC-AE=6,4-2,4=4(cm)
Ta có: ΔADE\(\sim\)ΔACB
nên DE/CB=AD/AC=3,2/6,4=1/2
=>DE=1,8(cm)

A B C E D
a) Xét \(\Delta ABE\) và \(\Delta DCE\) có :
BE = EC (E là trung điểm của BC -gt)
\(\widehat{AEB}=\widehat{DEC}\) (đối đỉnh)
AE = ED (gt)
=> \(\Delta ABE\) = \(\Delta DCE\) (c.g.c)
b) Ta có : \(\widehat{CDE}=\widehat{BAE}\) (2 góc tương ứng - \(\Delta ABE\) = \(\Delta DCE\) )
Mà 2 góc này ở vị trí so le trong
=> AB //DC (đpcm)
c) Theo giả thuyết thì ta có :
Trong tam giác ABC có : \(AB=AC\)
=> \(\Delta ABC\) cân tại A
Mà AE là đường trung tuyến trong tam giác
=> AE đồng thời là đường trung trưc trong tam giác
=> \(AE\perp BC\) (đpcm)
d) Để \(\widehat{ADC}=45^o\)
<=> \(\Delta ABC\) vuông cân tại A
Xét tam giác \(\Delta ABC\) và \(\Delta ADC\) có:
\(\begin{array}{l}AB = AD(gt)\\BC = DC(gt)\\AC\,\,\,chung\end{array}\)
Suy ra \(\Delta ABC = \Delta ADC\)(c.c.c)
Xét 2 tam giác ABC và tam giác ADC ta có :
AB = AD
BC = DC
AC chung
=> ΔABC = ΔADC