Vẽ hình và viết giả thiết, kết luận của định lí:
“Hai góc đối đỉnh thì bằng nhau”
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

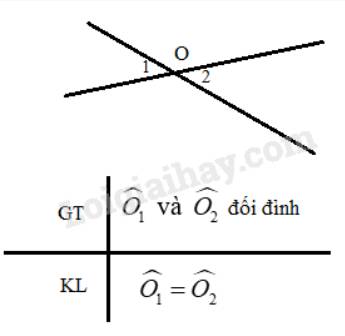

a)
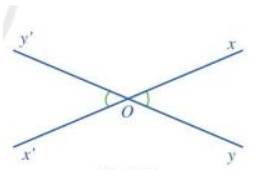
b)
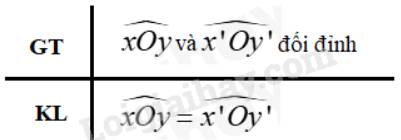
c) Vì góc xOy và x’Oy’ là hai góc đối đỉnh nên Oy và Oy’ là hai tia đối nhau; Ox và Ox’ là hai tia đối nhau
\( \Rightarrow \widehat {xOy}\) và \(\widehat {xOy'}\) là hai góc kề bù; \(\widehat {xOy'}\) và \(\widehat {x'Oy'}\) là hai góc kề bù
\( \Rightarrow \widehat {xOy} + \widehat {xOy'} = 180^\circ \); \(\widehat {xOy'} + \widehat {x'Oy'} = 180^\circ \) ( tính chất 2 góc kề bù)
\( \Rightarrow \)\(\widehat {xOy} = \widehat {x'Oy'}\) (đpcm)

O 1 2 3
| Giả thiết | Góc O1 và góc O3 đối đỉnh |
| Kết luận | Góc O1 = Góc O3 |
C/m :
Ta có :
\(\begin{cases}\widehat{O_1}+\widehat{O_2}=180^0\\\widehat{O_3}+\widehat{O_2}=180^0\end{cases}\) ( kề bù )
\(\Rightarrow\begin{cases}\widehat{O_1}=180^0-\widehat{O_2}\\\widehat{O_3}=180^0-\widehat{O_2}\end{cases}\)
\(\Rightarrow\widehat{O_1}=\widehat{O_3}\left(đpcm\right)\)

GT KL đường thẳng a;b cắt nhau tại O góc O 1 và O 2 đối đỉnh góc O góc O 1 = 2 a b O 1 2 3
Vì góc O1 và góc O2 kề bù => O1 + O2 = 180o
Góc góc O2 và góc O3 kề bù => O2 + O3 = 180o
=> O1 = O2

a: Giả thiết: a//b
Kết luận: \(\widehat{A_1}=\widehat{B_1}\)

a:
| GT | góc AOB và góc COD là hai góc đối đỉnh |
| KL | góc AOB=góc COD |
b:
| GT | a\(\perp\)b, c\(\perp\)b |
| KL | a//c |

Định lí: "Hai góc cùng phụ một góc thứ ba thì bằng nhau".
Hình vẽ:
O123
Giả thiết - Kết luận:
| GT |
\widehat{O_1} + \widehat{O_2} = 90^{\circ}O1+O2=90∘ \widehat{O_2} + \widehat{O_3} = 90^{\circ}O2+O3=90∘ |
| KL | \widehat{O_1} = \widehat{O_3}O1=O3 |
Định lí: "Hai góc cùng phụ một góc thứ ba thì bằng nhau".
Hình vẽ:
O123
Giả thiết - Kết luận:
| GT |
\widehat{O_1} + \widehat{O_2} = 90^{\circ}O1+O2=90∘ \widehat{O_2} + \widehat{O_3} = 90^{\circ}O2+O3=90∘ |
| KL | \widehat{O_1} = \widehat{O_3}O1=O3 |