Một trang trại cần thuê xe vận chuyển 450 con lợn và 35 tấn cám. Nơi cho thuê xe chỉ có 12 xe lớn và 10 xe nhỏ. Một chiếc xe lớn có thể chở 50 con lợn và 5 tấn cám. Một chiếc xe nhỏ có thể chở 30 con lợn và 1 tấn cám. Tiền thuê một xe lớn là 4 triệu đồng, một xe nhỏ là 2 triệu đồng. Hỏi phải thuê bao nhiêu xe mỗi loại để chi phí thuê xe là thấp nhất?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Gọi x; y lần lượt là số xe loại M, loại F cần thuê
Từ bài toán ta được hệ bất phương trình
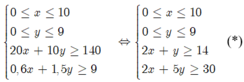
Tổng chi phí T(x; y) = 4x+ 3y (triệu đồng)
Bài toán trở thành là tìm x; y nguyên không âm thoả mãn hệ (*) sao cho T( ;xy) nhỏ nhất.
Từ đó ta cần thuê 5 xe hiệu M và 4 xe hiệu F thì chi phí vận tải là thấp nhất.

- Gọi số xe loại A và loại B cần dùng là x và y xe .
=> Số tiền là : \(T=4x+3y\)
Mà \(\left\{{}\begin{matrix}20x+10y\ge140\\0,6x+1,5y\ge9\end{matrix}\right.\) và \(\left\{{}\begin{matrix}x\ge0\\y\ge0\end{matrix}\right.\)
Ta có :

Mỗi xe lớn chở được 15 tấn. Mỗi xe nhỏ chở được 10 tấn.
Giải thích các bước giải:
Gọi x(tấn) là số tấn hàng mỗi xe lớn chở được, y(tấn) là số tấn hàng mỗi xe nhỏ chở được.ĐK: x > 0; y > 0 ; x > y
Một xe tải lớn chở 3 chuyến và xe tải nhỏ chở 4 chuyến thì chuyển được tất cả 85 tấn hàng Theo đề bài ta có phương trình: 3x + 4y = 85. 4 chuyến xe tải lớn chở nhiều hơn 5 chuyến xe tải nhỏ 10 tấn ta có phương trình:4x – 5y = 10
Hệ phương trình: Ta được ( x =15 ; y = 10 ) thoả mãn ĐKVậy: Mỗi xe lớn chở được 15 tấn. Mỗi xe nhỏ chở được 10 tấn.

Gọi `x` là tải trọng của xe tải lớn và `y` là tải trọng của xe tải nhỏ `(tấn;x,y>0)`
`-` Vì tất cả chở 84 tấn hàng nên: `6x+4y=84` `(1)`
`-` Và vì mỗi xe tải lớn chở nhiều hơn xe tải nhỏ là 4 tấn nên: `x-y=4` `(2)`
Từ `(1)` và `(2)` ta có hệ phương trình:
\(\left\{{}\begin{matrix}6x+4y=84\\x-y=4\end{matrix}\right.\)
Giải hệ phương trình ta được: \(\Leftrightarrow\left\{{}\begin{matrix}x=10\\y=6\end{matrix}\right.\) (nhận)
Vậy, tải trọng của xe tải lớn là `10` tấn và xe tải nhỏ là `6` tấn.
