Cho Hình 3.44. Giải thích tại sao:
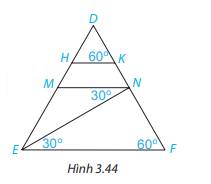
a) MN//EF
b) HK//EF
c) HK//MN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QT
1
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
a) Vì \(\widehat {xAB} = \widehat {ABy}( = 45^\circ )\)
Mà hai góc này ở vị trí so le trong
Do đó, xx’ // By ( Dấu hiệu nhận biết 2 đường thẳng song song) hay Ax’ // By
b)
Cách 1:
Vì Ax’ // By nên \(\widehat{x'HK}=\widehat{HKB}\) (2 góc so le trong)
Mà \(\widehat{x'HK}=90^0\) nên \(\widehat{HKB}=90^0\)
Do đó, Ax’ \( \bot \) HK
Cách 2:
Vì Ax’ // By, mà By \( \bot \) HK nên Ax’ \( \bot \) HK (đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì vuông góc với đường thẳng kia)
5 tháng 9 2021
\(a,b,\) Ta có \(\left\{{}\begin{matrix}AN=BN\\AM=CM\end{matrix}\right.\Rightarrow MN\) là đtb \(\Delta ABC\Rightarrow MN//BC;MN=\dfrac{1}{2}BC\left(1\right)\)
Ta có \(\left\{{}\begin{matrix}BE=EG\\CG=GF\end{matrix}\right.\Rightarrow EF\) là đtb \(\Delta BGC\Rightarrow EF//BC;EF=\dfrac{1}{2}BC\left(2\right)\)
\(\left(1\right)\left(2\right)\Rightarrow EF=MN;EF//MN\)
\(c,d,\) Cmtt câu a,b, ta được \(NE,MF\) lần lượt là đtb \(\Delta AGB;\Delta AGC\)
\(\Rightarrow\left\{{}\begin{matrix}NE=\dfrac{1}{2}AG;NE//AG\\MF=\dfrac{1}{2}AG;MF//AG\end{matrix}\right.\Rightarrow NE=MF;NE//MF\)
MP
25 tháng 8 2023
Ta có: \(\dfrac{MN}{HK}=\dfrac{9}{4}\)
\(\Rightarrow\dfrac{18}{HK}=\dfrac{9}{4}\)
\(\Rightarrow9.HK=18.4\)
\(\Rightarrow9HK=72\)
\(\Rightarrow HK=8cm\)
9 tháng 8 2021
a, vì BM,CN là các trung tuyến=>AN=NB
và AM=MC=>MN là đường trung bình tam giác ABC
=>MN//BC(1)
\(=>MN=\dfrac{1}{2}BC=6cm\)
b, có H,K theo theo thứ tự là trung điểm của BG và CG.
=>GH=HB và GK=KC
=>HK là đường trung bình tam giác GBC=>HK//BC(2)
(1)(2)=>HK//MN
=>\(HK=\dfrac{1}{2}BC=>HK=MN\left(=\dfrac{1}{2}BC\right)\)
24 tháng 9 2020
a) Xét ΔABC có
N là trung điểm của AB(CN là đường trung tuyến ứng với cạnh AB của ΔABC)
M là trung điểm của AC(BN là đường trung tuyến ứng với cạnh AC của ΔABC)
Do đó: MN là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
⇒MN//BC và \(MN=\frac{BC}{2}\)(Định lí 2 về đường trung bình của tam giác)(1)
Xét ΔGBC có
H là trung điểm của GB(gt)
K là trung điểm của GC(gt)
Do đó: HK là đường trung bình của ΔGBC(Định nghĩa đường trung bình của tam giác)
⇒HK//BC và \(HK=\frac{BC}{2}\)(Định lí 2 về đường trung bình của tam giác)(2)
Từ (1) và (2) suy ra MN//HK và MN=HK(đpcm)
b) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=9^2+12^2=225\)
\(\Leftrightarrow BC=\sqrt{225}=15cm\)
\(\Leftrightarrow2\cdot HK=15cm\)
hay \(HK=\frac{15cm}{2}=7.5cm\)
Vậy: HK=7,5cm
AR
3
LD
7 tháng 7 2017
Sửa đề: NK cắt MH tại I.
I N M H K O F
a) Ta có:
góc INM + góc KNM = 180 độ ( 2 góc kề bù)
góc IMN + góc HMN = 180 độ ( 2 góc kề bù)
góc KNM = góc HMN ( định nghĩa hình thang cân NMHK)
=> góc INM = góc IMN
=> tam giác INM cân tại I.
b) Gọi F là trung điểm của NM.
Xét tam giác INM cân tại I có IF là đường trung tuyến cũng là đường cao và là đường phân giác
=> IF vuông góc với NM tại F (1)
Xét tam giác NMK và tam giác MNH ta có:
NM là cạnh chung
góc MNK = góc NMH ( định nghĩa hình thang cân NMHK)
NK = MH ( tính chất hình thang cân NMHK)
=> tam giác NMK = tam giác MNH ( c - g - c)
=> góc NMK = góc MNH ( 2 góc tương ứng)
=> tam giác ONM cân tại O
Mà Ò là đường trung tuyến nên cũng là đường cao
=> OF vuông góc với NM tại F (2)
Từ (1) và (2) suy ra IF trùng với OF ( Tiên đề Ơ - clit)
=> I, F, O thẳng hàng
Ta có:
góc IKH = góc IHK ( định nghĩa hình thang cân NMHK)
LD
7 tháng 7 2017
mình bổ sung câu trả lời
Ta có:
góc IKH = góc IHK ( định nghĩa hình thang cân NMHK)
=> tam giác IKH cân tại I
Mà IO là đường phân giác cũng là đường cao
Nên IO vuông góc với HK (đpcm)
a) Vì \(\widehat {MNE} = \widehat {NEF}( = 30^\circ )\), mà 2 góc này ở vị trí so le trong nên MN//EF ( Dấu hiệu nhận biết 2 đường thẳng song song.)
b) Vì \(\widehat {DKH} = \widehat {DFE}( = 60^\circ )\), mà 2 góc này ở vị trí đồng vị nên HK//EF ( Dấu hiệu nhận biết 2 đường thẳng song song.)
c) Vì MN//EF; HK//EF nên HK//MN