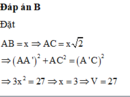(a-b)10/(c-d)10=3a3+2b3/3c3+2d3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
A.3a3 B.a3 C.a3
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 11 2021
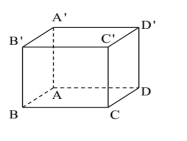
Gọi H là hình chiếu vuông góc của A' lên (ABCD)
Do \(A'A=A'B=A'D\) \(\Rightarrow H\) trùng tâm đường tròn ngoại tiếp tam giác ABD
\(\Rightarrow H\) là trung điểm BD
\(AC=\sqrt{AB^2+AD^2}=2a\)\(\Rightarrow AH=\dfrac{1}{2}AC=a\)
\(\Rightarrow A'H=\sqrt{A'A^2-AH^2}=a\sqrt{3}\)
\(\Rightarrow V=A'H.AB.AD=3a^3\)
Q
23 tháng 10 2018
1) Theo tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{b}=\frac{c}{d}=\frac{a+b}{c+d}=\frac{a-b}{c-d}\Leftrightarrow\frac{a+b}{a-b}=\frac{c+d}{c-d}\)
2) Theo tính chất dãy tỉ số bằng nhau ta có:
\(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a^{10}}{b^{10}}=\frac{c^{10}}{d^{10}}=\frac{a^{10}+b^{10}}{c^{10}+d^{10}}=\frac{a^{10}-b^{10}}{c^{10}-d^{10}}\Leftrightarrow\frac{a^{10}+b^{10}}{a^{10}-b^{10}}=\frac{c^{10}+d^{10}}{c^{10}-d^{10}}\)
HD
1
AH
Akai Haruma
Giáo viên
9 tháng 11 2021
Lời giải:
Vì $a,b,c$ không âm và $a+b+c=2\Rightarrow 0\leq a,b,c\leq 2$
Khi đó:
$a\leq 12a$
$2b^2=2b.b\leq 4b\leq 12b$
$3c^3=3c^2.c\leq 3.2^2.c=12c$
$\Rightarrow P=a+2b^2+3c^3\leq 12(a+b+c)=24$
Vậy $P_{\max}=24$ khi $(a,b,c)=(0,0,2)$
TA
2
VM
9 tháng 11 2019
a) Ta có: \(\frac{a}{b}=\frac{c}{d}.\)
\(\Rightarrow\frac{a}{c}=\frac{b}{d}\)
\(\Rightarrow\frac{5a}{5c}=\frac{8b}{8d}.\)
Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\frac{5a}{5c}=\frac{8b}{8d}=\frac{5a+8b}{5c+8d}\) (1)
\(\frac{5a}{5c}=\frac{8b}{8d}=\frac{5a-8b}{5c-8d}\) (2)
Từ (1) và (2) \(\Rightarrow\frac{5a+8b}{5c+8d}=\frac{5a-8b}{5c-8d}.\)
\(\Rightarrow\frac{5a+8b}{5a-8b}=\frac{5c+8d}{5c-8d}\left(đpcm\right).\)
b) Ta có: \(\frac{a}{b}=\frac{c}{d}.\)
\(\Rightarrow\frac{a}{c}=\frac{b}{d}\)
\(\Rightarrow\frac{a^{10}}{c^{10}}=\frac{b^{10}}{d^{10}}.\)
Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\frac{a^{10}}{c^{10}}=\frac{b^{10}}{d^{10}}=\frac{a^{10}+b^{10}}{c^{10}+d^{10}}.\)
\(\Rightarrow\frac{a^{10}}{c^{10}}=\frac{a^{10}+b^{10}}{c^{10}+d^{10}}\left(đpcm\right).\)
Chúc bạn học tốt!
9 tháng 11 2019
a) Có: \(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a}{c}=\frac{b}{d}=\frac{5a+8b}{5c+8d}=\frac{5a-8b}{5c-8d}\\ \Rightarrow\frac{5a+8b}{5a-8b}=\frac{5c+8d}{5c-8d}\)
b) Có: \(\frac{a}{c}=\frac{b}{d}\Rightarrow\frac{a^{10}}{c^{10}}=\frac{b^{10}}{d^{10}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
\(\frac{a^{10}}{c^{10}}=\frac{b^{10}}{d^{10}}=\frac{a^{10}+b^{10}}{c^{10}+d^{10}}\)
22 tháng 8 2021
Bài 3:
a: Ta có: \(\left(y-5\right)\left(y+8\right)-\left(y+4\right)\left(y-1\right)\)
\(=y^2+8y-5y-40-y^2+y-4y+4\)
=-36
b: Ta có: \(y^4-\left(y^2-1\right)\left(y^2+1\right)\)
\(=y^4-y^4+1\)
=1
22 tháng 8 2021
Bài 2:
a: \(\left(2a-b\right)\left(4a+b\right)+2a\left(b-3a\right)\)
\(=8a^2+2ab-4ab-b^2+2ab-6a^2\)
\(=2a^2-b^2\)
b: \(\left(3a-2b\right)\left(2a-3b\right)-6a\left(a-b\right)\)
\(=6a^2-9ab-4ab+6b^2-6a^2+6ab\)
\(=6b^2-7ab\)
c: \(5b\left(2x-b\right)-\left(8b-x\right)\left(2x-b\right)\)
\(=10bx-5b^2-16bx+8b^2+2x^2-xb\)
\(=3b^2-7xb+2x^2\)
CM
13 tháng 1 2017
Chọn B
Mà ∠ B = ∠ A + 10 ° (2)
nên từ (1) và (2) => ∠ C - 10 ° = ∠ A + 10 ° => ∠ C = ∠ A + 20 °
Ta có: ∠ D = ∠ C + 10 ° => ∠ D = ∠ A + 20 ° + 10 ° => ∠ D = ∠ A + 30 °
Ta có : ∠ A+ ∠ B+ ∠ C+ ∠ D = 360 ° ( tổng bốn góc của tứ giác)
=> ∠ A+ ∠ A + 10 ° + ∠ A + 20 ° + ∠ A + 30 ° = 360 °
=> 4 ∠ A + 60 ° = 360 °
Do đó: ∠ A= 75 °
=> ∠ B = ∠ A + 75 ° + 10 ° = 85 °
=> ∠ C= ∠ A+ 20 ° = 95 °
=> ∠ D= ∠ A+ 30 ° = 105 °