Cho tam giác ABC cân tại A. Qua điểm M nằm giữa A và B kẻ đường thẳng song song với BC, cắt cạnh AC tại N. Chứng minh tam giác AMN cân.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 8 2023
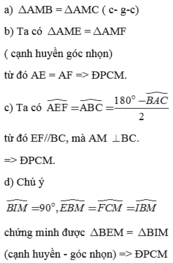
a: Xét ΔAMN có
Ax vừa là đường cao, vừa là phân giác
=>ΔAMN cân tại A
b: BE//AC
=>góc BEM=góc ANE
=>góc BEM=góc BME
=>BE=BM
Xét ΔDEB và ΔDNC có
góc DBE=góc DCN
DB=DC
góc BDE=góc NDC
=>ΔDEB=ΔDNC
=>BE=NC
=>BE=CN
23 tháng 8 2021
a: Xét ΔABC có
N là trung điểm của BC
NK//AB
Do đó: K là trung điểm của AC
Xét ΔABC có
N là trung điểm của BC
K là trung điểm của AC
Do đó: NK là đường trung bình của ΔBAC
Suy ra: \(NK=\dfrac{1}{2}AB\left(1\right)\)
b: Xét ΔABC có
N là trung điểm của BC
M là trung điểm của AB
Do đó: NM là đường trung bình của ΔABC
Suy ra: \(NM=\dfrac{AC}{2}\left(2\right)\)
Ta có: ΔBAC cân tại A
nên \(AB=AC\left(3\right)\)
Từ \(\left(1\right),\left(2\right),\left(3\right)\) suy ra NM=NK
Xét ΔNMK có NM=NK
nên ΔNMK cân tại N
19 tháng 3 2020
Mk thấy đề sai hay sao ý ko có đường thẳng nào đi qua B song song vs CD và cắt DM cả
19 tháng 3 2020
mik thấy cô ghi đè s mik ghi lại y chang chứ mik ko bik j cả. mik đọc cx thấy sai sai cái j á mà ko bik mik đọc đè đúng hay là sai nên mik mới đăng
26 tháng 6 2023
a: Xét ΔMBC và ΔMDA có
góc MCB=góc MAD
MC=MA
góc BMC=góc DMA
=>ΔMBC=ΔMDA
b: Xét ΔAMB và ΔCMD có
MA=MC
góc AMB=góc CMD
MB=MD
=>ΔAMB=ΔCMD
=>AB=CD
=>CA=CD
=>ΔCAD cân tại C
c: góc BCD=góc BAD
góc BCE=180 độ-góc ACB
=góc ABC+góc BAC
=góc ACB+góc BAC
=góc CAD+góc BAC
=góc BAD
=>góc BCD=góc BCE
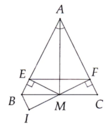
d: Xét ΔEBD có
EM là trung tuyến
EC=2/3EM
=>C là trọng tâm
=>DC đi qua trung điểm của BE
28 tháng 2 2020
b1 :
DE // AB
=> góc ABC = góc DEC (đồng vị)
góc ABC = góc ACB do tam giác ABC cân tại A (gt)
=> góc DEC = góc ACB
=> tam giác DEC cân tại D (dh)
b2:
a, tam giác ABC => góc A + góc B + góc C = 180 (đl)
góc A = 80; góc B = 50
=> góc C = 50
=> góc B = góc C
=> tam giác ABC cân tại A (dh)
b, DE // BC
=> góc EDA = góc ABC (slt)
góc DEA = góc ECB (dlt)
góc ABC = góc ACB (Câu a)
=> góc EDA = góc DEA
=> tam giác DEA cân tại A (dh)
Ta có tam giác ABC cân mà MN // BC. Nên \(\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\)(đồng vị)
Mà \(\widehat {ABC} = \widehat {ACB}\)(tam giác ABC cân) nên \(\widehat {AMN} = \widehat {ANM}\).
Vậy tam giác AMN cân tại A ( Tam giác có 2 góc bằng nhau)