Cho hai tam giác ABC và A’B’C’ thỏa mãn: AB = A’B’, \(\widehat A = \widehat {A'},\widehat C = \widehat {C'}\). Hai tam giác ABC và A’B’C’ có bằng nhau không? Vì sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
17 tháng 9 2023
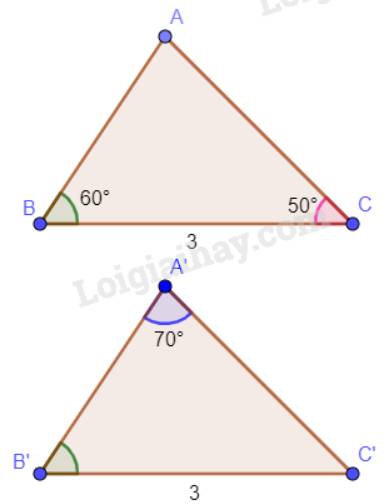
Tổng ba góc trong một tam giác bằng 180°. Vậy trong tam giác A’B’C’ có \(\widehat {C'} = 180^\circ - 70^\circ - 60^\circ = 50^\circ \).
Xét hai tam giác ABC và A’B’C’ có:
\(\widehat B = \widehat {B'} = 60^\circ ;\)
BC = B’C’ ( = 3 cm)
\(\widehat C = \widehat {C'} = 50^\circ \)
Vậy \(\Delta ABC = \Delta A'B'C'\)(g.c.g)
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
BC = B’C’ = 4 (đường chéo của 4 ô vuông).
Tam giác ABC và tam giác A’B’C’ có: BC = B’C’, AB = A’B’, \(\widehat B = \widehat {B'}\).
Vậy \(\Delta ABC = \Delta A'B'C'\)(c.g.c)
HQ
Hà Quang Minh
Giáo viên
17 tháng 9 2023
BC = B’C’ = 6 (ô vuông).
Tam giác ABC và A’B’C’ có các cặp cạnh tương ứng bằng nhau nên tam giác ABC bằng tam giác A’B’C’ (c.c.c)
KV
17 tháng 9 2023
Xét hai tam giác vuông: ∆ABC và ∆A'B'C' có:
BC = B'C' = 5 cm
AB = A'B' = 3 cm
⇒ ∆ABC = ∆A'B'C' (cạnh huyền - cạnh góc vuông)
⇒ AC = A'C' (hai cạnh tương ứng)
17 tháng 9 2023
Tam giác ABC và tam giác MNP bằng nhau (có ba cặp cạnh bằng nhau: AB = MN, BC = NP, AC = MP). Nên các cặp góc tương ứng trong hai tam giác này bằng nhau: \(\widehat A = \widehat M,\widehat B = \widehat N,\widehat C = \widehat P\).
Vậy \(\widehat A = \widehat M = 65^\circ \); \(\widehat B = \widehat N = 71^\circ \); \(\widehat C = \widehat P = 180^\circ - 65^\circ - 71^\circ = 44^\circ \)(vì tổng ba góc trong một tam giác bằng 180°).
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
- Độ dài các cạnh tương ứng của 2 tam giác ABC và A’B’C’ bằng nhau.
- Hai tam giác ABC và A'B'C' có bằng nhau.
- Độ dài các cạnh AB' và AC' của hai tam giác em vừa vẽ có bằng các cạnh AB' và AC' của hai tam giác các bạn khác vẽ.
- Hai tam giác em vừa vẽ có bằng hai tam giác mà các bạn khác vẽ.
CM
11 tháng 4 2017
* Trong tam giác vuông A’B’C’ có ∠ A ' = 90 0
Áp dụng định lí Pi-ta-go, ta có: A ' B ' 2 + A ' C ' 2 = B ' C ' 2
Suy ra: A ' C ' 2 = B ' C ' 2 - A ' B ' 2 = 15 2 - 9 2 = 144
Suy ra: A’C’ = 12 (cm)
* Trong tam giác vuông ABC có ∠ A = 90 0
Áp dụng định lí Pi-ta-go, ta có: B C 2 = A B 2 + A C 2 = 6 2 + 8 2 =100
Suy ra: BC = 10 (cm)
Ta có: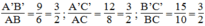 
Suy ra: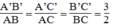 
Vậy △ A’B’C’ đồng dạng ΔABC (c.c.c)
Vì \(\widehat A = \widehat {A'},\widehat C = \widehat {C'}\)mà tổng ba góc trong một tam giác bằng 180° nên \(\widehat B = \widehat {B'}\).
Xét hai tam giác ABC và A’B’C’ có: \(\widehat A = \widehat {A'}\), AB = A’B’, \(\widehat B = \widehat {B'}\).
Vậy \(\Delta ABC = \Delta A'B'C'\)(g.c.g)