Giải thích bài toán ở phần mở đầu.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chữ đã viết trên tờ giấy ở hình bên là gì chữ “MẮT”.
Có hiện tượng trên là do chữ “MẮT” đặt trước gương sẽ cho ảnh ảo như trên.

Độ cao các thửa ruộng so với mực nước biển tạo thành một cấp số cộng với số hạng đầu u1 = 1 250 m và công sai d = 1,2 (m).
Khi đó công thức tổng quát của cấp số cộng là: un = u1 + (n – 1).d = 1 250 + (n – 1).1,2.
Vậy độ cao của thửa ruộng thứ 10 so với mực nước biển là:
u10 = 1 250 + (10 – 1).1,2 = 1 260,8 m.

Độ dài đèo Hải Vân là:
\(6,28:\frac{{157}}{{500}} = \frac{{157}}{{25}}.\frac{{500}}{{157}} = \frac{{3135}}{{157}} \approx 20\,\left( {km} \right)\)

+ Khi chưa đổ nước vào bát, ta không nhìn thấy đầu dưới (A) của chiếc đũa.
+ Trong không khí, ánh sáng chỉ có thể đi theo đường thẳng từ A đến mắt. Nhưng những điểm trên chiếc đũa thẳng đã chắn mất đường truyền đó nên tia sáng này không đến được mắt.
+ Giữ nguyên vị trí đặt mắt và đũa. Đổ nước vào bát tới một vị trí nào đó, ta lại nhìn thấy A.
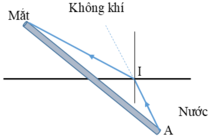
+ Hình vẽ trên cho thấy không có tia sáng đi theo đường thẳng nối A với mắt. Một tia sáng AI đến mặt nước, bị khúc xạ đi được tới mắt nên ta nhìn thấy A.
Thực ra người quan sát không nhìn thấy được đầu đũa A mà nhìn thấy ảnh của đầu đũa qua hiện tượng khúc xạ ánh sáng.

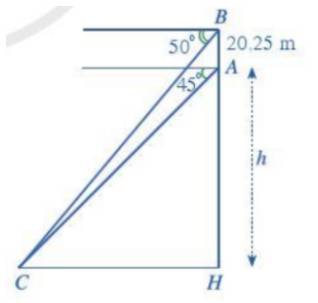
\(\left\{ \begin{array}{l}\widehat {ACH} = {45^o}\\\widehat {BCH} = {50^o}\end{array} \right.\) (hai góc đồng vị)
Mà \(\tan \widehat {ACH} = \frac{{AH}}{{CH}} \Rightarrow \tan {45^o} = \frac{h}{{CH}} \Leftrightarrow CH = h\)
Lại có: \(\tan \widehat {BCH} = \frac{{BH}}{{CH}} \Rightarrow \tan {50^o} = \frac{{h + 20,25}}{h}\)
\(\begin{array}{l} \Leftrightarrow h.\tan {50^o} = h + 20,25\\ \Leftrightarrow h = \frac{{20,25}}{{\tan {{50}^o} - 1}} \approx 105,6\end{array}\)
Vậy chiều cao của đỉnh Lũng cú so với chân núi là khoảng 105,6m.

Góc tạo bởi tòa tháp Capital Gate so với phương nằm ngang (mặt đất) là góc \(\widehat B\).
Ta có:
\(\widehat B + 90^\circ + 18^\circ = 180^\circ \) (tổng ba góc của một tam giác).
Suy ra: \(\widehat B = 180^\circ - 90^\circ - 18^\circ = 72^\circ \)
Vậy góc tạo bởi tòa tháp Capital Gate so với phương nằm ngang có số đo là 72°.


Xét hai tam giác ABC và ABD có: \(\widehat {CAB} = \widehat {DAB} = 60^\circ ,\widehat {ABC} = \widehat {ABD} = 45^\circ \), AB chung.
Vậy \(\Delta ABC = \Delta ABD\) (g.c.g).
Suy ra AC = AD và BC = BD ( 2 cạnh tương ứng)