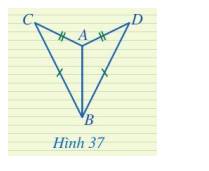
Hai tam giác ở Hình 37 có bằng không? Vì sao?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
4 tháng 3 2019
ΔABC và ΔADC có
AC chung
Góc ACB = góc DCB
BC = DC
⇒ ΔABC = ΔADC ( cạnh – góc – cạnh)
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
a) Xét \(\Delta{ABC}\) và \(\Delta{EDC}\), ta có:
AC = CE
\(\widehat {ACB}\)= \(\widehat {DCE}\) ( 2 góc đối đỉnh )
CB = CD
\(\Rightarrow \Delta{ABC}=\Delta{EDC}\) (c.g.c)
b) Ta thấy 2 tam giác ABC và BDE không bằng nhau vì
\(AC \ne BE;BC \ne BD;DE \ne AC\)
GL
21 tháng 9 2023
* Hình 14a:
Xét ∆ABC và ∆EDC có:
BC = DC (giả thiết);
^ACB = ^ECD (hai góc đối đỉnh);
AC = EC (giả thiết).
Do đó ∆ABC = ∆EDC (c.g.c).
* Hình 14b:
Không có cạnh nào của tam giác ABC bằng với cạnh của tam giác EBD nên hai tam giác này không bằng nhau.
Vậy Hình 14a có ∆ABC = ∆EDC (c.g.c); Hình 14b hai tam giác ABC và EBC không bằng nhau.
NM
3 tháng 3 2021
Hai tam giác đồng dạng chưa chắc sẽ bằng nhau còn khi 2 tam giác bằng nhau thì chắc chắn chúng sẽ đồng dạng. giải thích : Hai Δ có ti số đồng dạng là 1/2 hay 1/3 thì sẽ không bằng nhau tại vì 2 tam giác bằng nhau sẽ có tỉ lệ là 1:1
B
3 tháng 3 2021
Hai tam giác đồng dạng với nhau nếu một trong hai cặp góc và một cặp cạnh tương ứng bằng nhau. ... Vì vậy, nếu hai tam giác bằng nhau, thì cạnh và góc bên thứ ba cũng bằng nhau
Hai tam giác đồng dạng với nhau nếu một trong hai cặp góc và một cặp cạnh tương ứng bằng nhau. Cơ sở của lý thuyết này là tính chất tổng 3 góc trong tam giác. Theo tính chất tổng góc, tổng ba góc trong một tam giác là 180°. Vì vậy, nếu hai tam giác bằng nhau, thì cạnh và góc bên thứ ba cũng bằng nhau
CM
31 tháng 7 2017
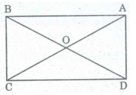
Gọi O là giao điểm 2 đường chéo hình chữ nhật ABCD.
Ta có: OA = OB = OC = OD (tính chất hình chữ nhật)
△ OAB = △ OCD (c.g.c) ⇒ S O A B = S O C D (1)
△ OAD = △ OBC (c.g.c) ⇒ S O A D = S O B C (2)
Kẻ AH ⊥ BD
S O A D = 1/2 AH.OD
S O A B = 1/2 AH.OB
Suy ra: S O A D = S O A B (3)
Từ (1), (2) và (3) ⇒ S O A B = S O B C = S O C D = S O D A
CM
6 tháng 4 2018
Ta ghép như sau:
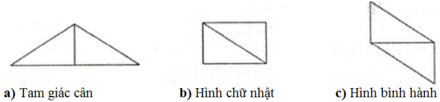
Diện tích 3 hình này đều bằng nhau vì cùng bằng tổng diện tích của hai tam giác vuông ban đầu.
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
a) Ta có:
\(\frac{{AF}}{{MN}} = \frac{b}{{3b}} = \frac{1}{3};\frac{{AE}}{{MG}} = \frac{c}{{3c}} = \frac{1}{3};\frac{{EF}}{{NG}} = \frac{a}{{3a}} = \frac{1}{3}\)
Xét tam giác \(AFE\) và tam giác \(MNG\) có:
\(\frac{{AF}}{{MN}} = \frac{1}{3};\frac{{AE}}{{MG}} = \frac{1}{3};\frac{{EF}}{{NG}} = \frac{1}{3} \Rightarrow \frac{{AF}}{{MN}} = \frac{{AE}}{{MG}} = \frac{{EF}}{{NG}}\)
Do đó, \(\Delta AFE\backsim\Delta MNG\) (c.c.c)
b) Tỉ số đồng dạng của tam giác \(AFE\) và tam giác \(MNG\) là \(\frac{1}{3}\).
Do đó, tỉ số chu vi của của tam giác \(AFE\) và tam giác \(MNG\) là \(\frac{1}{3}\) (tính chất)
Do đó, chu vi tam giác \(MNG\) là: \(15.3 = 45cm\)
Vậy chu vi tam giác \(MNG\) là 45 cm.
TP
14 tháng 12 2017
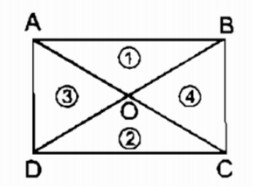
Gọi O là giao điểm hai đường chéo hình chữ nhật ABCD
⇒ OA = OB = OC = OD (tính chất hình chữ nhật)
∆ OAB = ∆ OCD (c.g.c) ⇒SOAB=SOCD⇒SOAB=SOCD (1)
∆ OAD = ∆ OBC (c.g.c) ⇒SOAD=SOBC⇒SOAD=SOBC (2)
Kẻ AH ⊥ BD
SOAD=\(\dfrac{1}{2}AH.OD\)
SOAB=\(\dfrac{1}{2}AH.OB\)
Suy ra: SOAD=SOAB (3)
Từ (1), (2) và (3) suy ra:
SOAB=SOBC=SOCD=SODA
TQ
1
15 tháng 5 2021
Hai tam giác bằng nhau thì đồng dạng
Hai tam giác đồng dạng thì chưa chắc bằng nhau
Xét tam giác ABC và tam giác ABD:
AC = AD; BC = BD, cạnh AB chung.
Vậy \(\Delta ABC = \Delta ABD\)(c.c.c)