Ku và Rio là hai con thuyềan có cùng vận tốc là 10 km/h khi nước Yên tĩnh. Tại cùng một thời điểm, Ku xuất phát từ A xuôi theo dòng nước, Rio xuất phát từ B gược dòng nước. Ku gặp Rio lần đầu tiên tại C , sau đó Ku tiếp tục đi đến B và ngay lập tức quay ngược trở lại, Rio tiếp tục đi đến A và cũng ngay lập tức quay ngược trở lại. Ku gặp Rio lần thứ hai tại D, cách A 18 km. Biết rằng vận tốc dòng nước không đổi và bằng 2 km/h, hỏi C cách A bao nhiêu km
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Công thức chuyển động: s = v.t
(s: quãng đường; v: vận tốc; t: thời gian).
Vận tốc xuôi dòng = vận tốc riêng + vận tốc dòng;
Vận tốc ngược dòng = vận tốc riêng – vận tốc dòng;
Các biểu thức thu được lần lượt là:
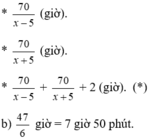

1. Thời gian bơi của vận động viên bằng thời gian trôi của quả bóng, vận tốc dòng nước bằng vận tốc của quả bóng trôi.
vn=vb=ACt=1,8(km/h)vn=vb=ACt=1,8(km/h)
Gọi vận tốc của vận động viên so với nước là v0v0, vận tốc so với bờ khi xuôi và ngược dòng là v1,v2v1,v2
⇒v1=v0+vnv2=v0−vn⇒v1=v0+vnv2=v0−vn
Thời gian bơi xuôi dòng:
t1=ABv1=ABv0−vn(1)t1=ABv1=ABv0−vn(1)
Thời gian bơi ngược dòng:
t2=CBv2=CBv0−vn(2)t2=CBv2=CBv0−vn(2)
Theo bài toán: t1+t2=13h(3)t1+t2=13h(3)
Từ (1),(2) và (3), ta có: v0=7,2km/hv1=9km/hv2=5,4km/hv0=7,2km/hv1=9km/hv2=5,4km/h
2. Tổng thời gian của vận động viên:
t3=ABvn≈0,83(h)1. Thời gian bơi của vận động viên bằng thời gian trôi của quả bóng, vận tốc dòng nước bằng vận tốc của quả bóng trôi.
vn=vb=ACt=1,8(km/h)vn=vb=ACt=1,8(km/h)
Gọi vận tốc của vận động viên so với nước là v0v0, vận tốc so với bờ khi xuôi và ngược dòng là v1,v2v1,v2
⇒v1=v0+vnv2=v0−vn⇒v1=v0+vnv2=v0−vn
Thời gian bơi xuôi dòng:
t1=ABv1=ABv0−vn(1)t1=ABv1=ABv0−vn(1)
Thời gian bơi ngược dòng:
t2=CBv2=CBv0−vn(2)t2=CBv2=CBv0−vn(2)
Theo bài toán: t1+t2=13h(3)t1+t2=13h(3)
Từ (1),(2) và (3), ta có: v0=7,2km/hv1=9km/hv2=5,4km/hv0=7,2km/hv1=9km/hv2=5,4km/h
2. Tổng thời gian của vận động viên:
t3=ABvn≈0,83(h)

Lời giải:
Gọi vận tốc cano khi nước yên lặng là $a$ km/h. Vận tốc cano lúc xuôi dòng là $a+4$ km/h, lúc ngược dòng là $a-4$ km/h
Thời gian cano đi quãng đường AB dài $24$ km rồi quay trở lại gặp bè gỗ tại điểm $C$ cách $A$ $8$ km là:
$\frac{AB}{v_{x}}+\frac{CB}{v_n}=\frac{24}{a+4}+\frac{24-8}{a-4}$ (h)
Thời gian này cũng chính là thời gian bè gỗ đi tới $C$.
Do đó:
$\frac{24}{a+4}+\frac{16}{a-4}=\frac{8}{4}=2$
$\Rightarrow a=20$ (km) (nhận) hoặc $a=0$ (km) (loại)
Vậy ............
Lúc đầu vì Ku đi xuôi dòng nước nên vận tốc của Ku lúc này là:
10 + 2 = 12 (km/h)
Lúc đầu vì Rio đi ngược dòng nước nên vận tốc của Rio lúc này là:
10 - 2 = 8 (km/h)
Tỉ số vận tốc giữa Ku và Rio lúc đầu là 12/8, nên khi Ku đi đến B thì Rio đã đi được 8/12 = 3/4 quãng đường. Lúc này Ku đang đi ngược dòng nước nên vận tốc của Ku là 10 - 2 = 8 (km/h), bằng vận tốc của Rio.
Do đó khi Rio đến A thì Ku đã đi được 1 + 1/4 = 5/4 quãng đường.
Lúc này Rio đi xuôi dòng nước nên vận tốc của Rio là 10 + 2 = 12 (km/h). Theo đề bài, AD = 18km nên thời gian để đi xuôi quãng đường AD là:
18/12 = 3/2 (giờ)
Tổng vận tốc của Ku và Rio lúc này là 12 + 8 = 20 (km/h), do đó khoảng cách giữa Ku và Rio lúc đó là:
20 x 3/2 = 30 (km)
Khoảng cách này bằng đúng 3/4 quãng đường ban đầu nên quãng đường ban đầu dài:
30 : 3/4 = 40 (km).
Quay trở lại thời điểm ban đầu, tổng vận tốc của Ku và Rio là:
12 + 8 = 20 (km/h)
Nên thời gian để Ku và Rio gặp nhau tại C là:
40 : 20 = 2 (giờ)
Khoảng cách AC bằng quãng đường Ku đi được trước khi gặp nhau tại C nên C cách A một khoảng cách là:
12 x 2 = 24 (km)