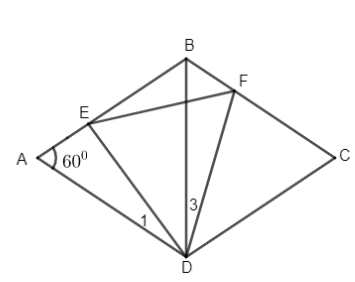
Cho hình thoi ABCD cạnh a có góc A = 60o. Trên các cạnh AB, BC, lần lượt lấy các điểm E, F sao cho BE + BF = a. Chứng minh rằng đường trung trực của đoạn thẳng EF luôn đi qua một điểm cố định khi E, F thay đổi trên AB, BC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 12 2021
giải
ta có AB=AD(gt)và góc A=60 độ nên tam giác DEF đều=>BD=AD
Tương tự tam giác DEF đều =>góc CBD=60độ
Từ BE+BF=BD=>AE=BF
Xét tam giác AED và tam giác BFD có:
AD=BD(cmt)
góc A=góc CBD=60 độ
AE=BF
Do đó tam giác AED=tam giác BFD(c,g.c)
=>DE=DF
nên tam giác DEF cân (1)
Và góc D1=góc D3 nên góc D1+góc EBD=60độ =>góc D3+góc EBD=60độ (2)
Từ (1) và (2) suy ra tam giác DEF đều.
2 tháng 12 2021
Ta có ABCD là hình thoi nên \(AD=AB\)
Mà \(\widehat{A}=60^0\) nên ABD đều
Lại có BD là phân giác \(\widehat{ABC}\Rightarrow\widehat{ABD}=\widehat{DBC}=60^0\)
\(\left\{{}\begin{matrix}BE+BF=BD=AB\\AE+BE=AB\end{matrix}\right.\Rightarrow AE=BF\)
\(\left\{{}\begin{matrix}AE=BF\\AD=BD\\\widehat{DAE}=\widehat{DBF}=60^0\end{matrix}\right.\Rightarrow\Delta DEA=\Delta DFB\left(c.g.c\right)\\ \Rightarrow DE=DF\)
Do đó DEF cân tại D
Mà \(\widehat{ADE}=\widehat{BDF}\left(\Delta DEA=\Delta DFB\right)\)
\(\Rightarrow\widehat{ADE}+\widehat{EDB}=\widehat{BDF}+\widehat{EDB}\\ \Rightarrow\widehat{ADB}=\widehat{EDF}=60^0\)
Vậy tam giác DEF đều
CM
20 tháng 3 2017
a) Do AM = DN Þ MADN là hình bình hành
⇒ D ^ = A M N ^ = E M B ^ = M B C ^
Ta có DMPE = DBPE nên EP = FP. Vậy MEBF là hình thoi và 2 điểm E, F đối xứng nhau qua AB.
b) Tứ giác MEBF có MB Ç EF = P; Lại có P trung điểm BM, P là trung điểm EF, MB ^ EF.
Þ MEBF là hình thoi.
c) Để BNCE là hình thang cân thì C N E ^ = B E N ^
Mà
C N E ^ = D ^ = M B C ^ = E B M ^ nên DMEB có 3 góc bằng nhau, suy ra điều kiện để BNCE là hình thang cân thì A B C ^ = 60 0
9 tháng 8 2023
Nếu D trùng B thì E sẽ trùng với A
=>Đường trung trực của DE là trung trực của AB
Nếu D trùng A thì E trùng với C
=>Đường ttrung trực của DE là trung trực của AC
Vẽ các đường trung trực của AB,AC, cắt nhau tại O
Gọi H,I lần lượt là trung điểm của AB,AC
=>OI vuông góc AC, OH vuông góc AB
Xét ΔOHB vuông tại H và ΔOIC vuông tại I có
OB=OC
HB=IC
=>ΔOHB=ΔOIC
=>OH=OI
ΔABC đều có O là giao của các đường trung trực
nên AO,BO lần lượt là phân giác của góc BAC, góc ABC
=>góc OAE=góc OBD=30 độ
=>ΔOAE=ΔOBD
=>OD=OE
=>O nằm trên trung trực của DE
=>ĐPCM