Nêu tính chất của phép nhân các số nguyên.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
QT
1
HQ
Hà Quang Minh
Giáo viên
16 tháng 9 2023
Tính chất giao hoán: \(a + b = b + a.\)
Tính chất kết hợp: \((a + b) + c = a + (b + c).\)
Cộng với số 0: \(a + 0 = 0 + a = a\).
Cộng với số đối: \(a + ( - a) = 0.\)
CM
19 tháng 4 2019
Ta đã biết tính chất kết hợp của phép nhân là:
(a.b).c = a.(b.c)
Từ đó ta có:
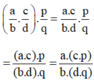
(áp dụng tính chất kết hợp của số nguyên cho cả tử và mẫu)
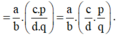
Vậy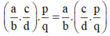 
(tính chất kết hợp của phép nhân phân số)
29 tháng 11 2021
1. Cộng, trừ cùng dấu:
Cộng (số nguyên dương) Vì hai số nguyên dương là những số tự nhiên nên cộng hai số nguyên dương chính là cộng hai số tự nhiên.
Cộng (số nguyên âm) Muốn cộng hai số nguyên âm ta cộng hai giá trị tuyệt đối của chúng rồi đặt dấu "-" trước kết quả.
Trừ : Muốn trừ hai số nguyên, ta lấy số bị trừ cộng cho số đối của số trừ
2. Nhân.
(Số âm) . (Số âm) = (Số dương)
LD
0
SG
3
16 tháng 4 2017
Các tính chất của phép cộng :
* a + b = b + a
* (a + b) + c = a + (b + c) = (a + c) + b
* a + 0 = 0 + a = a
Các tính chất của phép nhân :
* a.b = b.a
* (a.b).c = a.(b.c) = (a.c).b
* a.1 = 1.a
Tính chất của cả phép nhân lẫn phép cộng
* (a + b).c = a.c + b.c
16 tháng 4 2017
| Tên tính chất | Phép cộng | Phép nhân |
| Tính chất giao hoán | a + b = b + a | a.b = b.a |
| Tính chất kết hợp | a + (b + c) = (a + b) + c | a(b.c) = (a.b).c |
| Tính chất cộng với 0 | a + 0 = a | |
| Tính chất nhân với 1 | a.1 = a | |
| Tính chất phân phối |
a(b + c) = a.b + a.c |
a(b + c) = a.b + a.c |
Tính chất giao hoán: \(a.b = b.a.\)
Tính chất kết hợp: \((a.b).c = a.(b.c).\)
Nhân với số 1: \(a.1 = 1.a = a\).
Tính chất phân phối của phép nhân đối với phép cộng: \(a.(b + c) = a.b + a.c.\)