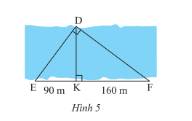
Người ta đo khoảng cách giữa hai điểm \(D\) và \(K\) ở hai bờ một dòng song (Hình 5). Cho biết \(KE = 90m,KF = 160m\). Tính khoảng cách \(DK\).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đổi: 1 km = 1000 m. Do đó AC = 1000 m.
Áp dụng định lí cosin trong tam giác ABC ta có:
\(A{B^2} = A{C^2} + B{C^2} - 2.AC.BC.\cos C\)
\(\begin{array}{l} \Rightarrow A{B^2} = {1000^2} + {800^2} - 2.1000.800.\cos {105^o}\\ \Rightarrow A{B^2} \approx 2054110,5\\ \Rightarrow AB \approx 1433,2\end{array}\)
Vậy khoảng cách AB là 1433,2 m.

Gọi d 1 , d ' 1 và d 2 , d ' 2 lần lượt là các khoảng cách từ hai khe đến thấu kính và từ thấu kính đến màn ở hai vị trí của thấu kính. Ta có :
d 1 + d ' 1 = d 2 + d ' 2 = D = 1,2 m = 120 cm và d 2 - d 1 =72 cm.
Theo tính chất trở lại ngược chiều của ánh sáng, ta biết rằng : d 2 = d ' 1 và d 1 = d ' 2
Do đó : d ' 1 - d 1 = d 2 - d ' 2 = d = 72 cm.
Ở một trong hai vị trí của thấu kính thì ảnh lớn hơn vật, còn ở vị trí kia thì ảnh nhỏ hơn. Mà ảnh lớn hơn vật khi d' > d. Vậy, ở vị trí thứ nhất thì ảnh lớn hơn và ta có :
d ' 1 - d 1 = 72 ; 2 d ' 1 = 120 + 72 ⇒ d ' 1 = 96 cm
d
1
= 120 - 96 = 24 cm và 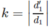 = 4
= 4
Khoảng cách giữa hai khe là :

Khoảng cách lớn nhất giữa 2 cây liên tiếp =45m, khi đó tổng số cây = 6
* * *
* * *

Xét tam giác OAB có:
M là trung điểm AO(gt)
N là trung điểm OB(gt)
=> MN là đường trung bình
\(\Rightarrow AB=2MN=2.45=90\left(m\right)\)

a: Sửa đề: \(\dfrac{KB}{KE}=\dfrac{KA}{KD}\)
\(\dfrac{KB}{KE}=\dfrac{7.2}{20.25}=\dfrac{16}{45}\)
\(\dfrac{KA}{KD}=\dfrac{6.4}{18}=\dfrac{16}{45}\)
Do đó: \(\dfrac{KB}{KE}=\dfrac{KA}{KD}\)
b: Xét ΔKDE có \(\dfrac{KB}{KE}=\dfrac{KA}{KD}\)
nên AB//DE
c: Xét ΔKDE có AB//DE
nên \(\dfrac{AB}{DE}=\dfrac{KB}{KE}\)
=>\(\dfrac{32}{DE}=\dfrac{16}{45}=\dfrac{32}{90}\)
=>DE=90(m)
- Xét tam giác \(DEF\) và tam giác \(KDF\) có:
\(\widehat F\) (chung)
\(\widehat {EDF} = \widehat {DKF} = 90^\circ \) (giải thuyết)
Suy ra, \(\Delta DEF\backsim\Delta KDF\) (g.g)
Suy ra, \(\widehat E = \widehat {KDF}\) (hai góc tương ứng).
- Xét tam giác \(DEK\) và tam giác \(FDK\) có:
\(\widehat E = \widehat {KDF}\) (chứng minh trên)
\(\widehat {EKD} = \widehat {FKD} = 90^\circ \) (giải thuyết)
Suy ra, \(\Delta DEK\backsim\Delta FDK\) (g.g)
Suy ra, \(\frac{{DK}}{{FK}} = \frac{{EK}}{{DK}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra, \(D{K^2} = EK.FK = 90.160 = 14400 \Rightarrow DK = \sqrt {14400} = 120\).
Vậy khoảng cách \(DK = 120m\).
\(DK^2=KE^2+KF^2=8100+25600=33700\)
\(\Rightarrow DK=10\sqrt[]{337}\left(m\right)\)