x + 3x+ 5x +7x +..+2023x=2023 x 2024
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2 tháng 8 2023
Có `xyz=2023=>2023=xyz`
Thay vào ta có :
\(\dfrac{xyz\cdot x}{xy+xyz\cdot x+xyz}+\dfrac{y}{yz+y+xyz}+\dfrac{z}{xz+z+1}=1\\ \dfrac{x^2yz}{xy\left(1+xz+z\right)}+\dfrac{y}{y\left(z+1+xz\right)}+\dfrac{z}{xz+z+1}=1\\ \dfrac{xz}{1+xz+z}+\dfrac{1}{z+1+xz}+\dfrac{z}{xz+z+1}=1\\ \dfrac{xz+1+z}{1+xz+z}=1\left(dpcm\right)\)
PN
2
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
17 tháng 12 2023
a, 7\(x\).(2\(x\) + 10) = 0
\(\left[{}\begin{matrix}x=0\\2x+10=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\2x=-10\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=-10:2\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
Vậy \(x\in\){-5; 0}
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
17 tháng 12 2023
b, - 9\(x\) : (2\(x\) - 10) = 0
- 9\(x\) = 0
\(x\) = 0
c, (4 - \(x\)).(\(x\) + 3) = 0
\(\left[{}\begin{matrix}4-x=0\\x+3=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=4\\x=-3\end{matrix}\right.\)
Vậy \(x\in\) {-3; 4}
d, (\(x\) + 2023).(\(x\) - 2024) = 0
\(\left[{}\begin{matrix}x+2023=0\\x-2024=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-2023\\x=2024\end{matrix}\right.\)
Vậy \(x\) \(\in\) {-2023; 2024}
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
17 tháng 12 2023
a, 7\(x\).(2\(x\) + 10) =0
\(\left[{}\begin{matrix}x=0\\2x+10=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\2x=-10\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=-5\end{matrix}\right.\)
Vậy \(x\in\) {-5; 0}
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
17 tháng 12 2023
b, -9\(x\) : (2\(x\) - 10) = 0
9\(x\) = 0
\(x\) = 0
c, (4 - \(x\)).(\(x\) + 3) = 0
\(\left[{}\begin{matrix}4-x=0\\x+3=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=4\\x=-3\end{matrix}\right.\)
Vậy \(x\in\) {-3; 4}
VH
1
26 tháng 2 2023
A= 7X³ + 3X⁴ - X² + 5X² - 6X³ - 2X⁴ - X³ + 2023
=> A= ( 3X⁴ - 2X⁴) + ( 7X³ - 6X³ - X³) + ( -X² + 5X²) + 2023
=> A= X⁴ + 3X² + 2023
11 tháng 4 2023
1. Giải:
Do \(5x+13B\in\left(2x+1\right)\Rightarrow5x+13⋮2x+1.\)
\(\Rightarrow2\left(5x+13\right)⋮2x+1\Rightarrow10x+26⋮2x+1.\)
\(\Rightarrow5\left(2x+1\right)+21⋮2x+1.\)
Do 5(2x+1)⋮2x+1⇒ Ta cần 21⋮2x+1.
⇒ 2x+1 ϵ B(21)=\(\left\{1;3;7;21\right\}.\)
Ta có bảng:
| 2x+1 | 1 | 3 | 7 | 21 |
| x | 0 | 1 | 3 | 10 |
| TM | TM | TM | TM |
Vậy xϵ\(\left\{0;1;3;10\right\}.\)
2. Giải:
Do (2x-18).(3x+12)=0.
⇒ 2x-18=0 hoặc 3x+12=0.
⇒ 2x =18 3x =-12.
⇒ x =9 x =-4.
Vậy xϵ\(\left\{-4;9\right\}.\)
3. S= 1-2-3+4+5-6-7+8+...+2021-2022-2023+2024+2025.
S= (1-2-3+4)+(5-6-7+8)+...+(2021-2022-2023+2024)+2025 Có 506 cặp.
S= 0 + 0 + ... + 0 + 2025.
⇒S= 2025.
TA
1
1 tháng 8 2023
x=2022
=>x+1=2023
A=x^50-x^49(x+1)+x^48(x+1)-...+x^2(x+1)-x(x+1)+x+2
=x^50-x^50-x^49+x^49+...+x^3+x^2-x^2-x+x+2
=2
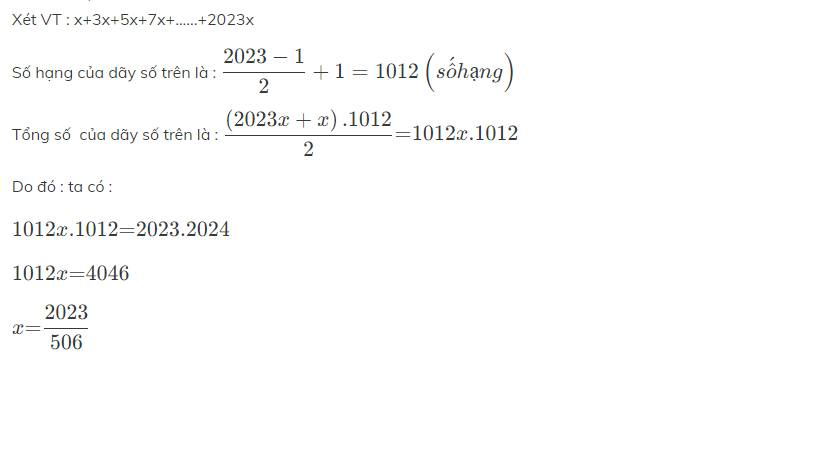
Xét VT : x+3x+5x+7x+......+2023x
Số hạng của dãy số trên là : \(\dfrac{2023-1}{2}+1=1012\left(sốhạng\right)\)
Tổng số của dãy số trên là : \(\dfrac{\left(2023x+x\right).1012}{2}\text{=}1012x.1012\)
Do đó : ta có :
\(1012x.1012\text{=}2023.2024\)
\(1012x\text{=}4046\)
\(x\text{=}\dfrac{2023}{506}\)
VT = x + 3x + 5x + 7x +... + 2023x = [(2023 - 1):2 +1] . (2023+1)x = 1012. 2024x = 2048288x
VP= 2023 . 2024= 4094552
VT=VP <=> 2048288x =4094552
<=>\(x\approx2\)