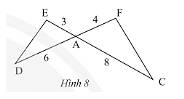
Cho tam giác \(ADE\) và tam giác \(ACF\) có các kích thước như trong Hình 8. Chứng minh rằng \(\Delta ADE\backsim\Delta ACF\).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
Vì \(\Delta ADE\backsim\Delta AMN\) nên \(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {ADE} = \widehat {AMN};\widehat {AED} = \widehat {ANM}\\\frac{{AD}}{{AM}} = \frac{{AE}}{{AN}} = \frac{{DE}}{{MN}}\end{array} \right.\)
Vì \(DE\) là đường trung bình của tam giác \(AMN\)nên \(DE = \frac{1}{2}MN\)
\( \Rightarrow \left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {ADE} = \widehat {AMN};\widehat {AED} = \widehat {ANM}\\\frac{{AD}}{{AM}} = \frac{{AE}}{{AN}} = \frac{{DE}}{{MN}} = \frac{1}{2}\end{array} \right.\)
\( \Rightarrow AM = 2AD;AN = 2AE;MN = 2DE\)
Lại có, \(\Delta AMN\backsim\Delta ABC\) nên \(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\\\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\end{array} \right.\)
Vì \(MN\) là đường trung bình của tam giác \(ABC\)nên \(MN = \frac{1}{2}BC\)
\(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\\\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}\end{array} \right.\)
\( \Rightarrow AB = 2AM;AC = 2AN;BC = 2MN\)
Vì tam giác \(\Delta ADE\backsim\Delta AMN,\Delta AMN\backsim\Delta ABC,\) nên \(\Delta ADE\backsim\Delta ABC\)
Tỉ số đồng dạng là: \(\frac{{AD}}{{AB}} = \frac{{\frac{{AM}}{2}}}{{2AM}} = \frac{1}{4}\).
Vậy tỉ số đồng dạng là \(\frac{1}{4}\).
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 4 2021
\(BE||DM\) (cùng vuông góc AC)
Theo định lý Talet: \(\left\{{}\begin{matrix}\dfrac{MK}{EH}=\dfrac{CK}{CH}\\\dfrac{DK}{BH}=\dfrac{CK}{CH}\end{matrix}\right.\) \(\Rightarrow\dfrac{MK}{EH}=\dfrac{DK}{BH}\)
\(\Rightarrow\dfrac{BH}{EH}=\dfrac{DK}{MK}\)
Hai tam giác vuông AHE và ACD đồng dạng (chung góc A) \(\Rightarrow\dfrac{AH}{AC}=\dfrac{AE}{AD}\Rightarrow AH.AD=AC.AE\)
Tương tự CHE đồng dạng CAF \(\Rightarrow\dfrac{CH}{AC}=\dfrac{CE}{CF}\Rightarrow CH.CF=AC.CE\)
\(\Rightarrow AH.AD+CH.CF=AC.AE+AC.CE=AC\left(AE+CE\right)=AC^2\) (1)
Lại có 2 tam giác vuông ACD và DCM đồng dạng (chung góc C)
\(\Rightarrow\dfrac{AC}{CD}=\dfrac{CD}{CM}\Rightarrow AC=\dfrac{CD^2}{CM}\Rightarrow AC^2=\dfrac{CD^4}{CM^2}\) (2)
(1); (2) suy ra đpcm
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
a) Xét tam giác \(ABC\) ta có:
\(DE//BC\) và \(D,E\) cắt \(AB;AC\) tại \(D;E\).
Do đó, \(\Delta ADE\backsim\Delta ABC\) (định lí)
b) Vì \(\Delta ADE\backsim\Delta ABC\) nên \(\frac{{AD}}{{AB}} = \frac{{DE}}{{BC}}\) (cách cặp cạnh tương ứng có cùng tỉ lệ).
Thay số, \(\frac{{16}}{{30}} = \frac{{22}}{{BC}} \Rightarrow BC = \frac{{22.30}}{{16}} = 41,25\)
Vậy \(BC = 41,25m\).
BL
2
28 tháng 3 2019
Xét tg ABD vuông tại D và tg ACE vuông tại E
có: ^A chung
=> tg ABD ~ tg ACE (gn)
=> \(\frac{AB}{AC}=\frac{AD}{AE}\Rightarrow\frac{AD}{AB}=\frac{AE}{AC}\)
xét tg ADE và tg ABC
có: AD/AB = AE/AC (cmt)
^A chung
=> tg ADE ~ tg ABC (c-g-c)
hình bn tự kẻ nha
CM
8 tháng 7 2019
Độ dài BM và MC đều là:
28 : 2 = 14(cm)
Diện tích hình tam giác EBM là:
(28 x 14) : 2 = 196 (cm2)
Diện tích hình tam giác DMC là:
(84 x 14) : 2 = 588 (cm2)
Diện tích hình tam giác EDM là:
1568 - (196 + 588) = 784 (cm2)
14 tháng 9 2023
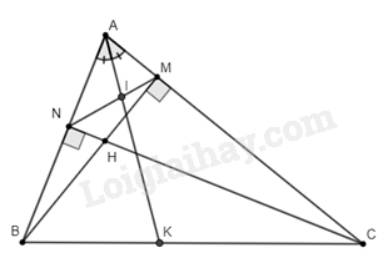
a) Vì \(BM\)là đường cao nên \(\widehat {AMB} = 90^\circ \); vì \(CN\)là đường cao nên \(\widehat {ANC} = 90^\circ \)
Xét tam giác \(AMB\) và tam giác \(ANC\) có:
\(\widehat A\) (chung)
\(\widehat {ANB} = \widehat {ANC} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta AMB\backsim\Delta ANC\) (g.g).
Suy ra, \(\frac{{AM}}{{AN}} = \frac{{AB}}{{AC}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Do đó, \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) (tỉ lệ thức)
Xét tam giác \(AMN\) và tam giác \(ABC\) có:
\(\widehat A\) (chung)
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) (chứng minh trên)
Suy ra, \(\Delta AMN\backsim\Delta ABC\) (c.g.c).
b) Xét tam giác \(AMN\) có \(AI\) là đường phân giác của \(\widehat {MAN}\left( {I \in MN} \right)\).
Theo tính chất đường phân giác ta có:
\(\frac{{IM}}{{IN}} = \frac{{AM}}{{AN}}\)
Xét tam giác \(ABC\) có \(AK\) là đường phân giác của \(\widehat {BAC}\left( {K \in BC} \right)\).
Theo tính chất đường phân giác ta có:
\(\frac{{BK}}{{KC}} = \frac{{AB}}{{AC}}\)
Mà \(\frac{{AM}}{{AN}} = \frac{{AB}}{{AC}}\) (chứng minh trên) nên \(\frac{{IM}}{{IN}} = \frac{{KB}}{{KC}}\) (điều phải chứng minh).
Ta có: \(\frac{{AE}}{{AF}} = \frac{3}{4};\frac{{AD}}{{AC}} = \frac{6}{8} = \frac{3}{4}\);
Xét \(\Delta ADE\) và \(\Delta ACF\) có:
\(\frac{{AE}}{{AF}} = \frac{{AD}}{{AC}} = \frac{3}{4}\)
\(\widehat {EAD} = \widehat {FAC}\) (hai góc đối đỉnh)
Do đó, \(\Delta ADE\backsim\Delta ACF\)(c.g.c)