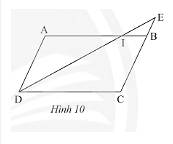
Trong Hình 10, cho biết \(ABCD\) là hình bình hành.
a) Chứng minh rằng \(\Delta IEB\backsim\Delta IDA\).
b) Cho biết \(CB = 3BE\) và \(AI = 9cm\). Tính \(DC\).
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
a) Xét tam giác \(MPQ\)có \(EF//MQ\) nên \(\Delta MPQ\backsim\Delta EPF\) (định lí) (1)
Xét tam giác \(MPQ\)có \(DC//MP\) nên \(\Delta MPQ\backsim\Delta DCQ\) (định lí) (2)
Từ (1) và (2) \(\Delta EPF\backsim\Delta DCQ\) (tính chất tam giác đồng dạng)
b) Xét tam giác \(EPF\)có \(IC//EP\) nên \(\Delta ICF\backsim\Delta EPF\) (định lí) (3)
Từ (1) và (3) suy ra, \(\Delta ICF\backsim\Delta MPQ\).
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
a) Vì \(MN//BC\) nên \(\widehat {MNB} = \widehat {ABC}\) (hai góc so le trong)
Vì \(MB//AC\) nên \(\widehat {MNB} = \widehat {ABC}\) (hai góc so le trong)
Xét tam giác \(BNM\) tam giác \(ABC\) ta có:
\(\widehat {MNB} = \widehat {ABC}\) (chứng minh trên)
\(\widehat {MNB} = \widehat {ABC}\) (chứng minh trên)
Do đó, \(\Delta BNM\backsim\Delta ABC\) (g.g)
b) Vì \(\Delta BNM\backsim\Delta ABC\) nên \(\widehat M = \widehat C = 48^\circ \) (hai góc tương ứng).
QT
1
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
a) Xét tam giác \(ABE\) có:
\(AB//CD\) và \(C,D\) cắt \(BE;AE\) lần lượt tại \(C,D\).
Do đó, \(\Delta AEB\backsim\Delta DEC\) (định lí)
b) Vì \(\Delta AEB\backsim\Delta DEC\) nên \(\frac{{AE}}{{ED}} = \frac{{AB}}{{CD}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Thay số ta được:
\(\frac{{x - 2}}{{10}} = \frac{3}{5} \Rightarrow x - 2 = \frac{{10.3}}{5} = 6 \Rightarrow x = 6 + 2 = 8\)
Vậy \(x = 8\).
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
a) Ta có: \(\Delta ABC\backsim\Delta A'B'C'\) thì \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\end{array} \right.\).
b) Xét tam giác \(DEF\) có:
\(\widehat D + \widehat E + \widehat F = 180^\circ \) (tổng ba góc trong một tam giác).
Ta có: \(\widehat D = 78^\circ ;\widehat E = 57^\circ \) thay số ta được
\(78^\circ + 57^\circ + \widehat F = 180^\circ \Rightarrow \widehat F = 180^\circ - 78^\circ - 57^\circ = 45^\circ \)
Ta có: \(\Delta DEF\backsim\Delta D'E'F' \Rightarrow \widehat D = \widehat {D'};\widehat E = \widehat {E'};\widehat F = \widehat {F'}\) (các góc tương ứng bằng nhau)
Do đó, \(\widehat D = \widehat {D'} = 78^\circ ;\widehat F = \widehat {F'} = 45^\circ \).
c) Ta có \(\Delta MNP\backsim\Delta M'N'P' \Rightarrow \frac{{MN}}{{M'N'}} = \frac{{MP}}{{M'P'}} = \frac{{NP}}{{N'P'}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Với \(MP = 10;NP = 6;M'N' = 15;N'P' = 12\) thay vào ta được:
\( \Rightarrow \left\{ \begin{array}{l}\frac{{MN}}{{15}} = \frac{1}{2}\\\frac{{10}}{{M'P'}} = \frac{1}{2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}MN = \frac{{15.1}}{2} = 7,5\\M'P' = \frac{{10.2}}{1} = 20\end{array} \right.\).
Vậy \(MN = 7,5;M'P' = 20\).
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
Ta có: \(\frac{{AE}}{{AF}} = \frac{3}{4};\frac{{AD}}{{AC}} = \frac{6}{8} = \frac{3}{4}\);
Xét \(\Delta ADE\) và \(\Delta ACF\) có:
\(\frac{{AE}}{{AF}} = \frac{{AD}}{{AC}} = \frac{3}{4}\)
\(\widehat {EAD} = \widehat {FAC}\) (hai góc đối đỉnh)
Do đó, \(\Delta ADE\backsim\Delta ACF\)(c.g.c)
15 tháng 9 2023
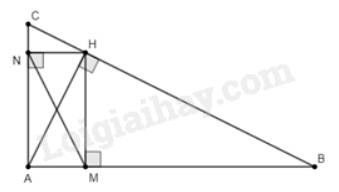
a) Xét \(\Delta AMH\) và \(\Delta AHB\) có:
\(\widehat {HAM}\) chung (do \(\widehat {HAM}\) cũng là \(\widehat {HAB}\))
\(\widehat {AMH} = \widehat {AHB} = 90^\circ \) (do \(HM \bot AB\) và \(AH\) là đường cao)
Do đó, \(\Delta AMH\backsim\Delta AHB\) (g.g).
b) Vì \(\Delta AMH\backsim\Delta AHB\) nên \(\frac{{AM}}{{AH}} = \frac{{AH}}{{AB}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra \(AM.AB = A{H^2}\) (1)
- Xét \(\Delta ANH\) và \(\Delta AHC\) có:
\(\widehat {HAN}\) chung (do \(\widehat {HAN}\) cũng là \(\widehat {HAC}\))
\(\widehat {ANH} = \widehat {AHC} = 90^\circ \) (do \(HN \bot AC\) và \(AH\) là đường cao)
Do đó, \(\Delta ANH\backsim\Delta AHC\) (g.g).
Vì \(\Delta ANH\backsim\Delta AHC\) nên \(\frac{{AN}}{{AH}} = \frac{{AH}}{{AC}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra \(AN.AC = A{H^2}\) (2)
Từ (1) và (2) suy ra, \(AM.AB = AN.AC\)(điều phải chứng minh).
c) Từ câu b ta có:
\(AM.AB = AN.AC \Rightarrow \frac{{AM}}{{AC}} = \frac{{AN}}{{AB}}\) (tỉ lệ thức)
Xét \(\Delta ANM\)và \(\Delta ABC\) ta có:
\(\widehat A\) chung
\(\frac{{AM}}{{AC}} = \frac{{AN}}{{AB}}\) (chứng minh trên)
Do đó, \(\Delta ANM\backsim\Delta ABC\)(c.g.c)
d) Áp dụng định lí Py- ta – go cho tam giác \(ABC\) vuông tại \(A\) ta có:
\(B{C^2} = A{B^2} + A{C^2} = {9^2} + {12^2} = 225 \Rightarrow BC = 15cm\)
Diện tích tam giác \(ABC\) là: \({S_{\Delta ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}AH.BC\)
\( \Rightarrow AH.BC = AB.AC\)
\( \Rightarrow AH = \frac{{AB.AC}}{{BC}} = \frac{{9.12}}{{15}} = 7,2cm\).
Ta có: \(A{H^2} = AM.AB = AM.9 = 7,{2^2} \Rightarrow AM = \frac{{7,{2^2}}}{9} = 5,76cm\)
\(A{H^2} = AN.AC = AN.12 = 7,{2^2} \Rightarrow AN = \frac{{7,{2^2}}}{{12}}4,32cm\).
Diện tích tam giác vuông \(AMN\) là:
\({S_{AMN}} = \frac{1}{2}AM.AN = \frac{1}{2}.5,76.4,32 = 12,4416c{m^2}\).
Vậy diện tích tam giác \(AMN\) là 12,4416cm2.
GH
31 tháng 7 2023
b
Δ ABD ⊥ tại D có DE là đường cao.
=> \(AD^2=AE.AB\) (hệ thức lượng) (1)
Δ ADC ⊥ tại C có DC là đường cao.
=> \(AD^2=AF.AC\) (hệ thức lượng) (2)
Từ (1), (2) suy ra: \(AE.AB=AF.AC\left(=AD^2\right)\)
Xét Δ AEF và Δ ACB có:
\(\widehat{EAF}=\widehat{CAB}\) (góc chung)
\(\dfrac{AF}{AE}=\dfrac{AB}{AC}\left(cmt\right)\)
=> Δ AEF đồng dạng Δ ACB (c.g.c)
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
Vì \(\Delta ADE\backsim\Delta AMN\) nên \(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {ADE} = \widehat {AMN};\widehat {AED} = \widehat {ANM}\\\frac{{AD}}{{AM}} = \frac{{AE}}{{AN}} = \frac{{DE}}{{MN}}\end{array} \right.\)
Vì \(DE\) là đường trung bình của tam giác \(AMN\)nên \(DE = \frac{1}{2}MN\)
\( \Rightarrow \left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {ADE} = \widehat {AMN};\widehat {AED} = \widehat {ANM}\\\frac{{AD}}{{AM}} = \frac{{AE}}{{AN}} = \frac{{DE}}{{MN}} = \frac{1}{2}\end{array} \right.\)
\( \Rightarrow AM = 2AD;AN = 2AE;MN = 2DE\)
Lại có, \(\Delta AMN\backsim\Delta ABC\) nên \(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\\\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\end{array} \right.\)
Vì \(MN\) là đường trung bình của tam giác \(ABC\)nên \(MN = \frac{1}{2}BC\)
\(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\\\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}\end{array} \right.\)
\( \Rightarrow AB = 2AM;AC = 2AN;BC = 2MN\)
Vì tam giác \(\Delta ADE\backsim\Delta AMN,\Delta AMN\backsim\Delta ABC,\) nên \(\Delta ADE\backsim\Delta ABC\)
Tỉ số đồng dạng là: \(\frac{{AD}}{{AB}} = \frac{{\frac{{AM}}{2}}}{{2AM}} = \frac{1}{4}\).
Vậy tỉ số đồng dạng là \(\frac{1}{4}\).
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
a) Xét \(\Delta ABD\) và \(\Delta CBD\)có:
DA=DC(gt)
BD chung
BA=BC
Vậy \(\Delta ABD = \Delta CBD\)(c.c.c)
b) Ta có \(\widehat A = \widehat C = {90^o}\)(hai góc tương ứng)
Theo định lí tổng ba góc trong tam giác BCD, ta có:
\(\begin{array}{l}\widehat C + \widehat {CDB} + \widehat {DBC} = {180^o}\\ \Rightarrow {90^o} + {30^o} + \widehat {DBC} = {180^o}\\ \Rightarrow \widehat {DBC} = {60^o}\end{array}\)
Mà \(\Delta ABD = \Delta CBD\) nên \(\widehat {ABD} = \widehat {CBD}\) ( 2 góc tương ứng)
\(\Rightarrow \widehat {ABD} = \widehat {CBD} = {60^o}\\\Rightarrow \widehat {ABC} = \widehat {ABD} + \widehat {CBD} = {60^o} + {60^o} = {120^o}\)
a) Do \(ABCD\) là hình bình hành nên \(BC//AD \Rightarrow EB//AD\)
Xét tam giác \(IDA\) có
\(EB//AD;EB\) cắt \(AI;ID\) tại \(B;E\).
Do đó, \(\Delta IEB\backsim\Delta IDA\) (định lí)
b) Ta có: \(\Delta IEB\backsim\Delta IDA \Rightarrow \frac{{IB}}{{IA}} = \frac{{BE}}{{DA}}\) (hai cặp cạnh tương ứng tỉ lệ).
Mà \(CB = AD;CB = 3BE \Rightarrow AD = 3BE;AI = 9\) nên ta có:
\(\frac{{IB}}{9} = \frac{{BE}}{{3BE}} = \frac{1}{3} \Rightarrow IB = \frac{{9.1}}{3} = 3\).
Vậy \(IB = 3cm.\)