Làm bằng công thức lớp 9 nha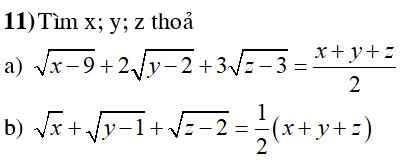 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 9 2023
Bài 6 :
Xét tam giác vuông AHC tại H có :
\(AC^2=AH^2+CH^2=144+25=169\)
\(\Rightarrow AC=13\left(cm\right)\)
\(sinC=\dfrac{AH}{AC}=\dfrac{12}{13}\)
\(sin^2C+cos^2C=1\Rightarrow cos^2C=1-sin^2C\)
\(\Rightarrow cos^2C=1-\dfrac{144}{169}=\dfrac{25}{169}\)
\(\Rightarrow cosC=\dfrac{5}{13}\left(cos>0\right)\)
\(sinB=sin\left(90^o-C\right)=cosC=\dfrac{5}{13}\)
12 tháng 9 2023
Bài 7 :
Ta có :
\(\widehat{B}+\widehat{C}=90^o\) (tam ABC vuông tại A)
\(\Leftrightarrow\widehat{C}=90^o-\widehat{B}=90^o-45^o=45^o\)
\(\Rightarrow\left\{{}\begin{matrix}sin\widehat{C}=sin45^o=\dfrac{\sqrt[]{2}}{2}\\cos\widehat{C}=cos45^o=\dfrac{\sqrt[]{2}}{2}\\tan\widehat{C}=tan45^o=1\\cot\widehat{C}=cot45^o=1\end{matrix}\right.\)
H9
HT.Phong (9A5)
CTVHS
14 tháng 9 2023
a) \(\sqrt{\dfrac{1}{8}}\cdot\sqrt{2}\cdot\sqrt{125}\cdot\sqrt{\dfrac{1}{5}}\)
\(=\dfrac{1}{\sqrt{8}}\cdot\sqrt{2}\cdot5\sqrt{5}\cdot\dfrac{1}{\sqrt{5}}\)
\(=\dfrac{\sqrt{2}}{2\sqrt{2}}\cdot\dfrac{5\sqrt{5}}{\sqrt{5}}\)
\(=\dfrac{1}{2}\cdot5\)
\(=\dfrac{5}{2}\)
b) \(4\sqrt{50}+2\sqrt{8}-4\sqrt{72}-\sqrt{32}\)
\(=4\cdot5\sqrt{2}+2\cdot2\sqrt{2}-4\cdot6\sqrt{2}-4\sqrt{2}\)
\(=20\sqrt{2}+4\sqrt{2}-24\sqrt{2}-4\sqrt{2}\)
\(=\left(20+4-24-4\right)\sqrt{2}\)
\(=-4\sqrt{2}\)
c) \(2\sqrt{20}-3\sqrt{45}+5\sqrt{80}-5\sqrt{5}\)
\(=2\cdot2\sqrt{5}-3\cdot3\sqrt{5}+5\cdot4\sqrt{5}-5\sqrt{5}\)
\(=4\sqrt{5}-9\sqrt{5}+20\sqrt{5}-5\sqrt{5}\)
\(=\left(20-9-5+4\right)\sqrt{5}\)
\(=10\sqrt{5}\)
d) \(2ab\sqrt{a^2b}-5a^2\sqrt{b^3}\) (\(a,b\ge0\))
\(=2ab\cdot\left|a\right|\sqrt{b}-5a^2\left|b\right|\sqrt{b}\)
\(=2a^2b\sqrt{b}-5a^2b\sqrt{b}\)
\(=\left(2a^2b-5a^2b\right)\sqrt{b}\)
\(=-3a^2b\sqrt{b}\)
e) \(\sqrt{40}+\sqrt{\dfrac{2}{5}}-\sqrt{\dfrac{5}{2}}\)
\(=2\sqrt{10}+\dfrac{\sqrt{10}}{5}-\dfrac{\sqrt{10}}{2}\)
\(=\dfrac{20\sqrt{10}}{10}+\dfrac{2\sqrt{10}}{10}-\dfrac{5\sqrt{10}}{10}\)
\(=\dfrac{\left(20+2-5\right)\sqrt{10}}{10}\)
\(=\dfrac{17\sqrt{10}}{10}\)
ST
7 tháng 6 2021
Tham khảo
DT xung quanh hình trụ:2πrh
DT toàn phần hình trụ:2πrh+2πr²
DT xung quanh hình nón:πrl
DTtoàn phần hình nón:πrl+πr²
Thể tích hình nón:1/3*πr²h
DT xung quanh hình nón cụt:π(r1+r2)l
Thể tích hình nón cụt:1/3*rh(r1²+r2²+r1*r2)
DT hình cầu :4πr²
thể tích hình cầu:4/3*πr²
VM
22 tháng 2 2016
gọi ngày n1 cần đề htcv là x (ngày)
ngày n2 cần để htcv là y (ngày)
(x,y>0)
trong 1ngày ng 1 làm đc 1/x (cv)
Trong 1ngày ng 2 làm đc 1/y (cv)
Trong một ngày cả hai người làm được 1/4 (cv)
=>> PT: 1/x + 1/y = 1/4 (1)
Trong 9 ngày ng 1 làm đc 9/x (cv)
theo đề ta có PT =>> 9/x + 1/4 = 1
Giải HPT ta đc: x = 12 ( ngày) ; y = 6 ( ngày)
Bạn thử giải lại coi có sai xót đâu ko hiumf mình =))
2 tháng 12 2016
nO2 = 0,672 / 22,4 = 0,03 mol
=> mO2 = 0,03 x 32 = 0,96 gam
Áp dụng định luật bảo toàn khối lượng
=> mY = mX - mO2 = 2,45 - 0,96 = 1.49 gam
=> mK = 1,49 x 52,35% = 0,780015 gam
=> nK = 0,780015 / 39 = 0,02 mol
=> mCl = 1,49 x 47,65% = 0,709985
=> nCl = 0,709985 / 35,5 = 0,02 mol
=> nK : nCl = 0,02 : 0,02 = 1 : 1
=> CTHH của Y: KCl
Theo định luật bảo toàn nguyên tố:
=> X chứa K, Cl, O
CTHH chung của X có dạng KClOx
PTHH: 2KClOx =(nhiệt)==> 2KCl + xO2
\(\frac{0,02}{x}\) ....................... 0,02
=> MKClOx = 2,45 / 0,02 = 122,5 (g/mol)
=> x = 3
=> CTHH của X là KClO3
19 tháng 8 2018
Giải:
Phân số chỉ số học sinh Lớp 6C là:
17/16 x 8/9 = 136/144 ( Lớp 6B )
Phân số chỉ số học sinh cả ba lớp 6 là:
144/144 + 8/9 + 136/144 = 408/144 ( Lớp 6B )
Số học sinh Lớp 6B là:
102 : 408/144 = 36 ( Học sinh )
Số học sinh Lớp 6A là:
36 x 8/9 = 32 ( Học sinh )
Số học sinh Lớp 6C là:
32 x 17/16 = 34 ( Học sinh )
Đáp số :
Lớp 6A: 32 Học sinh
Lớp 6B: 36 Học sinh
Lớp 6C: 34 Học sinh
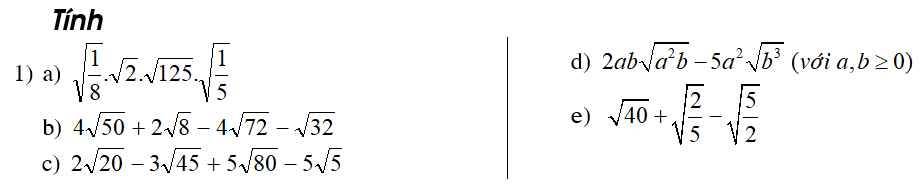
a) \(\sqrt[]{x-9}+2\sqrt[]{y-2}+3\sqrt[]{z-3}=\dfrac{x+y+z}{2}\left(1\right)\)
\(Đkxđ:\left\{{}\begin{matrix}x\ge9\\y\ge2\\z\ge3\end{matrix}\right.\)
Áp dụng Bất đẳng thức Bunhiacopxki :
\(\left(1\sqrt[]{x-9}+2\sqrt[]{y-2}+3\sqrt[]{z-3}\right)^2\le\left(1^2+2^2+3^2\right)\left(x-9+y-2+z-3\right)=14\left(x+y+z-14\right)\)
Dấu "=" xảy ra khi và chỉ khi :
\(\dfrac{x-9}{1}=\dfrac{y-2}{2}=\dfrac{z-3}{3}\left(a\right)\)
\(\left(1\right)\Leftrightarrow\)\(14\left(x+y+z-14\right)=\dfrac{\left(x+y+z\right)^2}{4}\left(2\right)\)
Đặt \(t=x+y+z\)
\(\Leftrightarrow14t-196=\dfrac{t^2}{4}\)
\(\Leftrightarrow t^2+56t-784=0\)
\(\Leftrightarrow\left(t-28\right)^2=0\)
\(\Leftrightarrow t=28\)
\(\Leftrightarrow x+y+z=28\)
\(\left(a\right)\Leftrightarrow\dfrac{x-9}{1}=\dfrac{y-2}{2}=\dfrac{z-3}{3}=\dfrac{x+y+z-14}{6}=\dfrac{28-14}{6}=\dfrac{7}{3}\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-9=1.\dfrac{7}{3}=\dfrac{7}{3}\\y-2=2.\dfrac{7}{3}=\dfrac{14}{3}\\z-3=3.\dfrac{7}{3}=7\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{34}{3}\\y=\dfrac{20}{3}\\z=10\end{matrix}\right.\)