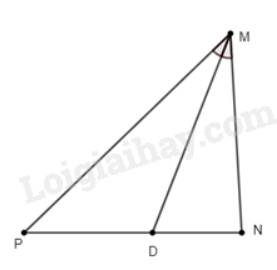
Cho \(\Delta ABC\) biết \(AM\) là đường phân giác. Trong các khẳng định sau, khẳng định nào đúng?
A. \(\frac{{BM}}{{MC}} = \frac{{AB}}{{AC}}\).
B. \(\frac{{AB}}{{MC}} = \frac{{BM}}{{AC}}\).
C. \(\frac{{AM}}{{MC}} = \frac{{AB}}{{AC}}\).
D. \(\frac{{BM}}{{MC}} = \frac{{AM}}{{AC}}\).

Chọn A
Chọn đáp án A
Vì \(AM\) là tia phân giác góc \(A\left( {M \in BC} \right)\) nên theo tính chất đường phân giác ta có:
\(\frac{{BM}}{{CM}} = \frac{{AB}}{{AC}};\frac{{BM}}{{AB}} = \frac{{CM}}{{AC}};\frac{{CM}}{{BM}} = \frac{{AC}}{{AB}};\frac{{AC}}{{CM}} = \frac{{AB}}{{BM}}\).