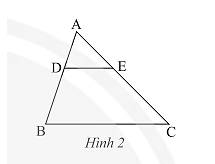
Cho tam giác \(ABC\), biết \(DE//BC\) (Hình 2). Trong các khẳng định sau, khẳng định nào sai?
A. \(\frac{{AD}}{{DB}} = \frac{{AE}}{{EC}}\).
B. \(\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}}\).
C. \(\frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}\).
D. \(\frac{{BD}}{{AB}} = \frac{{DE}}{{BC}}\).


Chọn D
Vì \(DE//BC\) nên theo định lí Thales và hệ quả của định lí Thales ta có:
\(\frac{{AD}}{{BD}} = \frac{{AE}}{{EC}};\frac{{BD}}{{AD}} = \frac{{EC}}{{AE}};\frac{{BD}}{{AB}} = \frac{{EC}}{{AC}};\frac{{AD}}{{AB}} = \frac{{AE}}{{AC}} = \frac{{DE}}{{BC}}\).