Hai ô tô khởi cùng lúc và cùng vận tốc 50 \(km/h\), một ô tô bắt đầu từ \(B\), một ô tô bắt đầu từ \(C\) và cùng đi về phía \(D\).a) Viết công thức của hai hàm số biểu thị khoảng cách từ \(A\) đến mỗi xe sau \(x\) giờ.b) Chứng tỏ đồ thị của hai hàm số trên là hai đường thẳng song...
Đọc tiếp
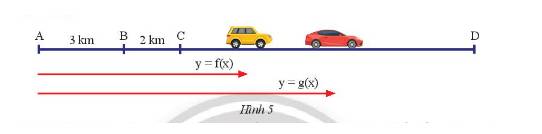
Hai ô tô khởi cùng lúc và cùng vận tốc 50 \(km/h\), một ô tô bắt đầu từ \(B\), một ô tô bắt đầu từ \(C\) và cùng đi về phía \(D\).
a) Viết công thức của hai hàm số biểu thị khoảng cách từ \(A\) đến mỗi xe sau \(x\) giờ.
b) Chứng tỏ đồ thị của hai hàm số trên là hai đường thẳng song song.
a)
- Quãng đường xe ô tô khởi hành từ \(B\) đi được sau khoảng thời gian \(x\left( h \right)\) với vận tốc 50 km/h là: \(s = v.t = 50.x\)
Khi đó, công thức biểu thị khoảng cách từ điểm \(A\) đến xe là:
\(y = {y_0} + v.t = 3 + 50.x\).
- Quãng đường xe ô tô khởi hành từ \(C\) đi được sau khoảng thời gian \(x\left( h \right)\) với vận tốc 50 km/h là: \(s = v.t = 50.x\)
Khi đó, công thức biểu thị khoảng cách từ điểm \(A\) đến xe là:
\(y = {y_0} + v.t = 5 + 50.x\).
b) Đồ thị của hai hàm số trên là hai đường thẳng phân biệt vì cắt \(Oy\) tại hai điểm phân biệt.
Hai đường thẳng đó song song với nhau vì hệ số góc của hai đường thẳng này bằng nhau (đều có \(a = 50\)).