Quan sát Hình 8 và gọi tên các vectơ:
a) Cùng phương với vectơ \(\overrightarrow x \);
b) Cùng hướng với vectơ \(\overrightarrow a \) ;
Ngược hướng với vectơ \(\overrightarrow u \).
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a) Ta có:
Giá của vectơ \(\overrightarrow {\rm{w}} \) trùng với giá của \(\overrightarrow x \)
Giá của vectơ \(\overrightarrow y \), \(\overrightarrow z \)song song với giá của \(\overrightarrow x \)
Suy ra các vectơ cùng phương với vectơ \(\overrightarrow x \) là \(\overrightarrow {\rm{w}} \), \(\overrightarrow y \)và \(\overrightarrow z \)
b) Ta có:
Vectơ \(\overrightarrow b \) có giá song song với vectơ \(\overrightarrow a \)và có cùng hướng từ trên xuống với vectơ \(\overrightarrow a \)nên vectơ \(\overrightarrow b \) cùng hướng với vectơ \(\overrightarrow a \)
c) Ta có:
Vectơ \(\overrightarrow v \) có giá song song với vectơ \(\overrightarrow u \)và ngược hướng từ dưới lên trên so với vectơ \(\overrightarrow u \)nên vectơ \(\overrightarrow v \) ngược hướng với vectơ \(\overrightarrow u \)

Hai vectơ \(\overrightarrow a \) và \(\overrightarrow {AB} \) cùng hướng: có giá song song và cùng hướng với nhau.
Hai vectơ \(\overrightarrow a \) và \(\overrightarrow x \) ngược hướng: có giá song song và ngược hướng với nhau.
Vectơ \(\overrightarrow z \) có giá song song với giá của vectơ \(\overrightarrow a \), ngược hướng với vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow z \) ngược hướng với nhau.
Vectơ \(\overrightarrow y \) có giá song song với giá của vectơ \(\overrightarrow a \), cùng hướng với vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow y \) cùng hướng với nhau.
Vectơ \(\overrightarrow b \) có giá không song song với giá của vectơ \(\overrightarrow a \) nên hai vectơ \(\overrightarrow a \) và \(\overrightarrow b \) không cùng phương với nhuau. Do vậy không xét chúng cùng hướng hay ngược hướng với nhau.

a) ABCD là hình thang nên AB//CD
Các vectơ cùng hướng với vectơ \(\overrightarrow {AB} \) là các vectơ có hướng từ trái qua phải nên đó là: \(\overrightarrow {DC} ,\overrightarrow {DM} ,\overrightarrow {MC} \)
b) \(\overrightarrow {DM} \)có hướng từ trái sang phải nên các vectơ ngược hướng với vectơ \(\overrightarrow {DM} \)là \(\overrightarrow {BA} ,\overrightarrow {MD} ,\overrightarrow {CM} ,\overrightarrow {CD} \)

A B C D O M N
a)
Các véc tơ cùng phương với \(\overrightarrow{AB}\) là:
\(\overrightarrow{MO};\overrightarrow{OM};\overrightarrow{MN};\overrightarrow{NM};\overrightarrow{NO};\overrightarrow{ON};\overrightarrow{DC};\overrightarrow{CD};\overrightarrow{BA};\overrightarrow{AB}\).
Hai véc tơ cùng hướng với \(\overrightarrow{AB}\) là:
\(\overrightarrow{MO};\overrightarrow{ON}\).
Hai véc tơ ngược hướng với \(\overrightarrow{AB}\) là:
\(\overrightarrow{OM};\overrightarrow{ON}\).
b) Một véc tơ bằng véc tơ \(\overrightarrow{MO}\) là: \(\overrightarrow{ON}\).
Một véc tơ bằng véc tơ \(\overrightarrow{OB}\) là: \(\overrightarrow{DO}\).

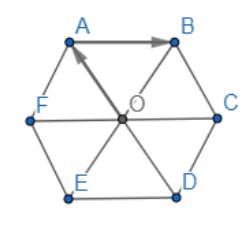
a) Ta có: AO // BC // EF
Suy ra các vectơ khác vectơ khác vectơ \(\overrightarrow 0 \) và cùng hướng với vectơ \(\overrightarrow {OA} \) là : \(\overrightarrow {DO} ,\overrightarrow {DA} ,\overrightarrow {CB} ,\overrightarrow {EF} \)
b) Ta có: \(OA = OB = OC = OD = OE = FO\) và AB // FC // ED
Suy ra các vectơ bằng vectơ \(\overrightarrow {AB} \) là \(\overrightarrow {FO} ,\overrightarrow {OC} ,\overrightarrow {ED} \)

Giá của vectơ \(\overrightarrow {AB} \) là đường thẳng AB
Giá của vectơ \(\overrightarrow {CD} \) là đường thẳng CD.
Giá của vectơ \(\overrightarrow {PQ} \) là đường thẳng PQ.
Dễ thấy: AB // CD và CD trùng PQ.

Giá của vectơ \(\overrightarrow {AB} \) là đường thẳng AB
Giá của vectơ \(\overrightarrow {CD} \) là đường thẳng CD.
Dễ thấy: đường thẳng AB trùng với đường thẳng CD.
Do đó hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) có cùng phương.
Lại có: vectơ \(\overrightarrow {AB} \) chỉ hướng đi về bên phải còn vectơ \(\overrightarrow {CD} \) chỉ hướng đi về bên trái.
Vậy hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) có ngược hướng.

a) Ta có:
Giá của vectơ \(\overrightarrow {AB} \) là đường thẳng AB
Giá của vectơ \(\overrightarrow {CD} \) là đường thẳng CD.
Dễ thấy: AB // CD do đó hai vectơ này cùng phương.
b) Quan sát hình 42, ta thấy cả hai vectơ \(\overrightarrow {AB} \) và \(\overrightarrow {CD} \) cùng hướng sang phải
Như vậy hai vectơ này cùng hướng.
c) Ta có: \(|\overrightarrow {AB} |\; = AB\); \(|\overrightarrow {CD} |\; = CD\) và AB = CD (cùng dài 5 ô vuông)
Vậy độ dài của hai vectơ là bằng nhau.


Gọi a, b, c là các đường thẳng lần lượt chứa các vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \).
Khi đó: a, b, c lần lượt là giá của các vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \)
a) Dễ thấy: a // b // c
\( \Rightarrow \) Ba vectơ \(\overrightarrow a ,\overrightarrow b ,\overrightarrow c \) cùng phương với nhau.
Vậy các cặp vectơ cùng phương là: \(\overrightarrow a \) và \(\overrightarrow b \), \(\overrightarrow a \) và \(\overrightarrow c \), \(\overrightarrow b \) và \(\overrightarrow c \).
b) Quan sát ba vectơ, ta thấy: vectơ \(\overrightarrow a \) và \(\overrightarrow c \) cùng hướng xuống còn vectơ \(\overrightarrow b \) hướng lên trên.
Vậy vectơ \(\overrightarrow a \) và \(\overrightarrow c \) cùng hướng, vectơ \(\overrightarrow a \) và \(\overrightarrow b \) ngược hướng, vectơ \(\overrightarrow b \) và \(\overrightarrow c \) ngược hướng.