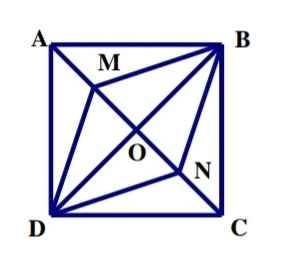
tính diện tích hình thoi MBND biết ABCD là hình vuông và 2 đường chéo của hình vuông AC = BD = 20cm (M là tâm điểm chính A;O;N là điểm giữa OC)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
L
linh
10 tháng 9 2023
Đúng(0)
Những câu hỏi liên quan
M
7 tháng 9 2023
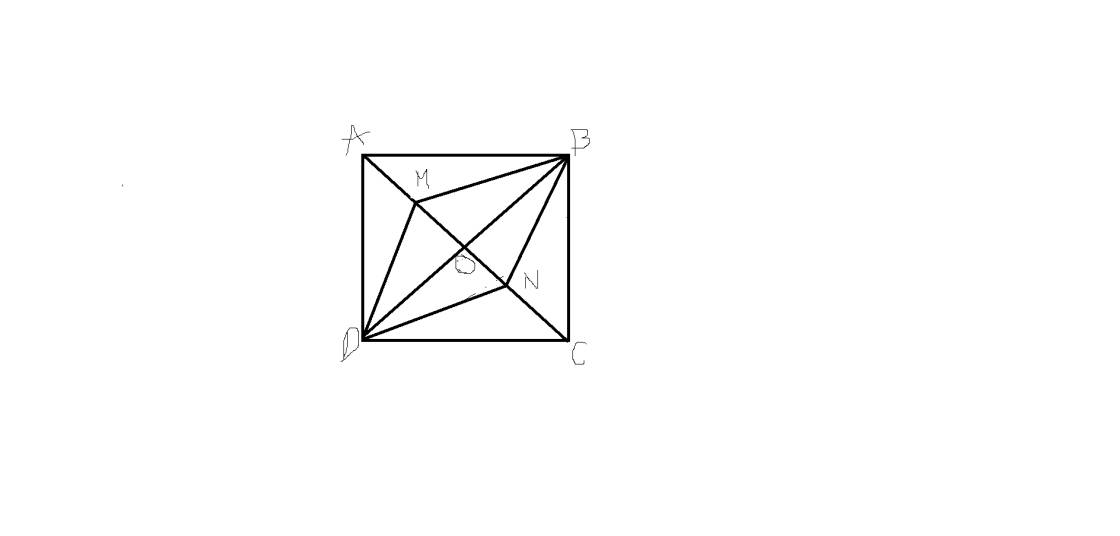
Để tính diện tích hình thoi MBND, ta cần biết độ dài hai cạnh của hình thoi.
Vì ABCD là hình vuông và AC=BD=20cm, ta có thể tính được độ dài các cạnh của hình thoi.
Vì M là điểm chính giữa AO, ta có AM = MO = AO/2 = 20/2 = 10cm.
Tương tự, vì N là điểm chính giữa OC, ta có CN = NO = OC/2 = 20/2 = 10cm.
Vậy, AM = MO = 10cm và CN = NO = 10cm.
Để tính diện tích hình thoi MBND, ta có công thức: Diện tích = (đường chéo 1 * đường chéo 2)/2.
Đường chéo 1 là AC = 20cm và đường chéo 2 là BD = 20cm.
Vậy, diện tích hình thoi MBND = (20 * 20)/2 = 200cm².
Vậy, diện tích hình thoi MBND là 200cm².
2 tháng 5 2018
Nối MB , BN , ND , DM ta có :
S NBO = 1/2 S ABO ( chung đường cao hạ từ B xuống AO , Đáy MO= AO )
S OBN = 1/2 S BOC ( chung đường cao hạ từ B xuống CO , Đáy NO= CO )
S ODN = 1/2 S ODC (chung đường cao hạ từ D xuống CO , Đáy NO= CO )
S DMO = 1/2 S ADO ( chung đường cao hạ từ D xuống AO , Đáy MO= AO )
Từ đó ta suy ra : SNBO + S OBN + S ODN + S DMO = 1/2 S ABO +1/2 S BOC + 1/2 S ODC + 1/2 S DMO = 1/2 S ABCD
Vậy S BMDN = 1/2 S ABCD
S BNDM = 52,7 : 2 = 26,35 cm2
ds 26,35 cm2
28 tháng 4 2021
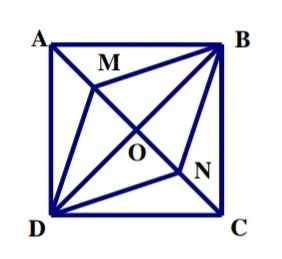
Ta có :chiều cao và độ dài đáy của mỗi hình tam giác trong hình bằng nhau .
=> Diện tích mỗi hình đó cũng bằng nhau .
Vì hình ABCD bằng với 8 hình tam giác nhỏ .
Mà hình MBND bằng với 4 hình tam giác nhỏ.
=> Diện tích hình là : 52,7 : 8 * 4 = 26,35 (cm2)
Đáp số: 26,35 cm2
( BẠN ĐỪNG TRÁCH MIK VÌ MIK LẤY Ở TRÊN MẠNG NHƯNG CŨNG VIẾT LẠI CHO BẠN XEM KẾT QUẢ VÀ THAM KHẢO)
Mong được bạn tk cho mik !
10 tháng 2 2020
Chưa học căn bậc thì thôi nhé!
Gọi chiều dài của cạnh hình vuông là: \(\sqrt{32}cm\)
Chiều dài đường chéo hình vuông là:
\(\sqrt{32+32}=\sqrt{64}=8cm\)
Bán kính hình tròn là:
\(8:2=4\left(cm\right)\)
Diện tích hình tròn là:
\(4\times4\times3,14=50,24\left(cm^2\right)\)
Đáp số: \(50,24cm^2\)
E
30 tháng 1 2022
1 cạnh của hình vuông là \(\sqrt{32}\)cm
Áp dụng định lí Pytago cho tam giác ACD
\(AC^2+CD^2=AD^2\)
=> \(AD=\sqrt{\left(\sqrt{32}\right)^2+\sqrt{\left(\sqrt{32}\right)^2}}=8\)cm
Bán kính đg tròn = 8: 2 = 4 ( cm )
Diện tích đg tròn
\(=R^2.3,14=4^2.3,14=50,24cm^2\)