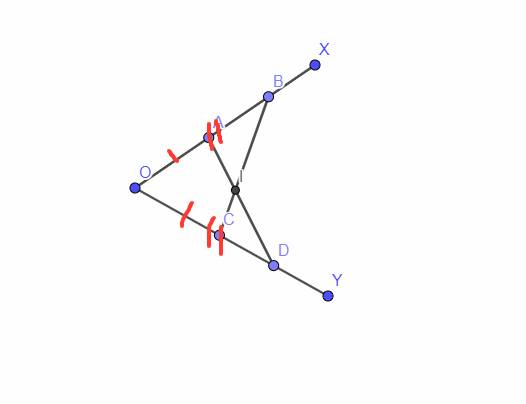
Cho góc nhọn xOy. trên tia Ox lấy 2 điểm A,B và trên tia Oy lấy 2 điểm C,D - sao cho OA=OC và OB=OD. Gọi I là giao điểm AD và CB.
a) Chứng minh BC=AD.
b) Chứng minh tam giác IAC cân và tam giác IDB cân.
c) Chứng minh OI là tia phân giác của BAC.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 7 2023
a: Xét ΔOCB và ΔOAD có
OC=OA
góc O chung
OB=OD
=>ΔOCB=ΔOAD
=>BC=AD
b: Xét ΔIAB và ΔICD có
góc IBA=góc IDC
AB=CD
góc IAB=góc ICD
=>ΔIAB=ΔICD
=>IA=IC và IB=ID
=>ΔIAC cân tại I và ΔIBD cân tại I
9 tháng 3 2023
\(\text{#TuanNam}\)
`a,` Mình xp sửa đề câu a: cm: Tam giác `OAD =` Tam giác `OCB (` vì nếu là `OCD` thì k đúng, vì `3` điểm đó thẳng hàng `)`.
Xét Tam giác `OAD` và Tam giác `OCB` có:
`OA=OC (g``t)`
\(\widehat{O}\) chung
`OB=OD (g``t)`
`=>` Tam giác `OAD =` Tam giác `OCB (c-g-c)`
`b,` Hnhu đề bị sai ;-;
`
HN
2 tháng 12 2021
a: Xét ΔOAD và ΔOCB có
OA=OC
ˆOO^ chung
OD=OB
Do đó: ΔOAD=ΔOCB
Suy ra: AD=CB