Cho phương trình \(x^2-x-2=0\)a, giải phương trình b, Vẽ hai đồi thị \(y=x^2\) và \(y=x+2\) trên cùng 1 toạ độ c, Chứng tỏ rằng hai nghiệm tìm được trong câu a là hoành độ giao điểm của hai đồ thị Sáng mai mình sẽ đăng bài giải. Ai có thể giài được trong hôm nay thì giúp mình nhé. Cảm ơn các bạn...
Đọc tiếp
Cho phương trình
\(x^2-x-2=0\)
a, giải phương trình
b, Vẽ hai đồi thị \(y=x^2\) và \(y=x+2\) trên cùng 1 toạ độ
c, Chứng tỏ rằng hai nghiệm tìm được trong câu a là hoành độ giao điểm của hai đồ thị
Sáng mai mình sẽ đăng bài giải. Ai có thể giài được trong hôm nay thì giúp mình nhé. Cảm ơn các bạn ạ
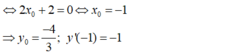
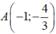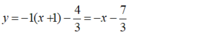
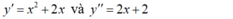
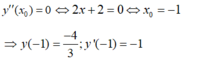
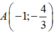là:
là: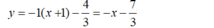
.
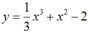
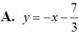
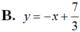
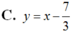
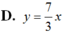
\(x^2-x-2=0\)
\(\Leftrightarrow x^2+x-2x-2=0\)
\(\Leftrightarrow x\left(x+1\right)-2\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(x-2\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x+1=0\\x-2=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=-1\\x=2\end{cases}}\)
a, Giải phương trình \(x^2-x-2=0\)
\(=''-1''^2-4\times1\times''-2''=1+8\) lớn hơn \(0\)
\(\sqrt{\Delta}=\sqrt{9}=3\)
\(\Rightarrow x_1=-1;x_2=2\)
b, Vẽ đồ thị bảng số
- Hàm số \(y=x^2\)
- Hàm số \(y=x+2\)
+ Cho \(x=0\Rightarrow2\) được điểm A '' 0,2 ''
+ Cho \(x=2\Rightarrow y=0\) được điềm '' -2 ; 0 ''
Đồi thị hàm số