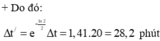Trong điều trị ung thư, bệnh nhân được chiếu xạ với một liều xác định nào đó từ một nguồn phóng xạ với chu kì bán rã là 4 năm. Khi nguồn được sử dụng lần đầu thì thời gian cho một lần chiếu xạ là Δt. Cứ sau 1 năm bệnh nhân phải tới bệnh viện khám bệnh và tiếp tục chiếu xạ. Tính Δt biết lần chiếu xạ thứ 4 chiếu trong thời gian 20 phút *
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HD
Hà Đức Thọ
Admin
19 tháng 5 2016
Số hạt phóng xạ cần dùng là: \(N=H.\Delta t\)
Vì sau 2 năm, liều lượng phóng xạ dùng như nhau nên:
\(H_0.\Delta t_0=H_1.\Delta t_1\)
\(\Rightarrow \Delta t_1=\dfrac{H_0}{H_1}.\Delta t_0\)
\(H_1=H_0/2^{\dfrac{t}{T}}\)
\(\Rightarrow \Delta t_1=2^\dfrac{t}{T}.\Delta t_0=2^\dfrac{2}{5,27}.10=...\)
VT
29 tháng 9 2019
Đáp án D
+ Gọi N 0 là số hạt của mẫu phóng xạ ban đầu.
Ban đầu ta có: 
+ Lần chiếu xạ thứ 4 ứng với thời gian là 3 tháng.
Số hạt của mẫu phóng xạ còn lại là: 
+ Để bệnh nhân nhận được lượng tia g như lần đầu tiên thì:
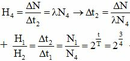
® D t 2 » 33,6 phút.
VT
4 tháng 12 2017
- Lượng tia γ phóng xạ lần đầu:
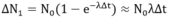
(áp dụng công thức gần đúng: Khi x << 1 thì 1-e-x ≈ x, ở đây coi Δt >> T nên 1 - e-λΔt = λΔt)
- Sau thời gian 2 tháng, một nửa chu kì t = T/2, Lượng phóng xạ trong nguồn phóng xạ sử dụng lần đầu còn:
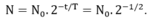
- Thời gian chiếu xạ lần này Δt’:
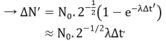
- Vì bệnh nhân được chiếu xạ với cùng một lượng tia γ như lần đầu nên ΔN' = ΔN. Do đó:
VT
10 tháng 3 2018
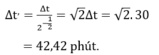
Đáp án D
+ Gọi N 0 là số hạt của mẫu phóng xạ ban đầu.
Ban đầu ta có
+ Lần chiếu xạ thứ 4 ứng với thời gian là 3 tháng.
Số hạt của mẫu phóng xạ còn lại là:
+ Để bệnh nhân nhận được lượng tia g như lần đầu tiên thì:
VT
19 tháng 8 2017
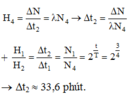
Đáp án: D.
Lượng tia γ phóng xạ lần đầu: ΔN1 = N0(1 - e-λDt) » N0λΔt
(áp dụng công thức gần đúng: Khi x << 1 thì 1 - e-x ≈ x, ở đây coi Δt >> T nên
1 - e-λ ∆ t = λ ∆ t)
Sau thời gian 2 tháng, một nửa chu kì t = T/2, Lượng phóng xạ trong nguồn phóng xạ sử dụng lần đầu còn:
N = N0.2-t/T = N0.2-1/2.
Thời gian chiếu xạ lần này ∆ t’ → ∆ N’ = N0.2-1/2(1 - e - λ ∆ t ' ) » N0.2-1/2 λ ∆ t’
Vì bệnh nhân được chiếu xạ với cùng một lượng tia γ như lần đầu nên ∆ N’ = ∆ N
Do đó 
phút.
VT
15 tháng 12 2017
Lượng tia γ phóng xạ lần đầu: ∆N1 = N0(1-e-λ∆t) ≈ N0λ∆t
(áp dụng công thức gần đúng: Khi x << 1 thì 1-e-x » x, ở đây coi ∆t >> T nên 1 - e-λDt = λDt)
Sau thời gian 2 tháng, một nửa chu kì t = T/2, Lượng phóng xạ trong nguồn phóng xạ sử dụng lần đầu còn: N1 = N0.2-t/T = N0.2-1/2
Thời gian chiếu xạ lần này Dt’ → ∆N’ = C(1-e-λ∆t’) ≈ N0.2-1/2λ∆t’
Vì bệnh nhân được chiếu xạ với cùng một lượng tia γ như lần đầu nên ∆N’ = ∆N
Do đó ∆t’= ∆t/2-1/2 = √2∆t = √2.30 = 42,42 phút.
Chọn đáp án D
