Cho hình thang ABCD (AB // CD) có \(\widehat {DAB} = \widehat {DBC}\)
a) Chứng minh rằng ΔABD ∽ ΔBDC
b) Giả sử AB=2cm,AD=3cm,BD=4cm. Tính độ dài các cạnh BC và DC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 4 2023
a: Xét ΔABD và ΔBDC có
góc DAB=góc CBD
góc ABD=góc BDC
=>ΔABD đồng dạng với ΔBDC
b: ΔABD đồng dạng ΔBDC
=>BA/BD=BD/DC
=>BD^2=4*9=36
=>BD=6cm
c: ΔABD đồng dạng với ΔBDC
=>\(\dfrac{S_{ABD}}{S_{BDC}}=\left(\dfrac{4}{6}\right)^2=\dfrac{4}{9}\)
=>\(S_{BDC}=32:\dfrac{4}{9}=72\left(cm^2\right)\)
CM
9 tháng 1 2019
a) Gợi ý: Lập tỉ số các cặp cạnh tương ứng và chứng minh chúng bằng nhau.
b) Từ phần a 
Þ ĐPCM
CM
25 tháng 5 2018
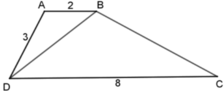
Vì ΔABD ⁓ ΔBDC nên A B B D = B D D C = A D B C , tức là 2 B D = B D 8 = 3 B C
Ta có B D 2 = 2.8 = 16 nên BD = 4 cm
Suy ra BC = 8.3 4 = 6 cm
Vậy BD = 4cm, BC = 6cm
Đáp án: D
CH
Cô Hoàng Huyền
Admin
VIP
13 tháng 7 2016
a. Ta thấy góc DAB = góc DBC (gt) và góc ABD = góc BDC (So le trong) nên \(\Delta DAB\sim\Delta CBD\left(g-g\right)\)
b. Ta có: \(\frac{DA}{BC}=\frac{AB}{BD}\Rightarrow\frac{3}{4}=\frac{5}{BD}\Rightarrow BD=\frac{20}{3}\)
\(\frac{AB}{BC}=\frac{BD}{DC}\Rightarrow DC=\frac{4.20}{3}:3=\frac{80}{9}\)
c. Ta thấy \(\frac{S_{ABD}}{S_{BDC}}=\left(\frac{3}{4}\right)^2=\frac{9}{16}\Rightarrow\frac{S_{ABD}}{S_{ABCD}}=\frac{9}{25}\Rightarrow S_{ABCD}=\frac{125}{9}\left(cm^2\right)\)
Chúc em học tốt :)
23 tháng 8 2020
a) Xét 2 tam giác ADB và BCD có:
góc DAB = góc DBC (gt)
góc ABD = góc BDC ( so le trong )
nên tam giác ADB đồng dạng với tam giác BDC.(1)
b) Từ (1) ta được AB/BC = DB/CD = AB/BD
hay ta có; AD/BC = AB/BD <==> 3,5/BC = 2,5/5
==> BC= 3,5*5/2,5 = 7 (cm)
ta cũng có: DB/CD = AB/BD <==> 5/CD = 2,5/5
==> CD = 5*5/2,5 =10 (cm)
c) Từ (1) ta được;
AD/BC = DB/CD = AB/BD hay 3.5/7 = 5/10 = 2,5/5 = 1/2 .
ta nói tam giác ADB đồng giạc với tam giác BCD theo tỉ số đồng dạng là 1/2
mà tỉ số diện tích bằng bình phương tỉ số động dạng
do đó S ADB/ S BCD = (1/2)^2 = 1/4
a) Có AB // CD => \(\widehat {AB{\rm{D}}} = \widehat {B{\rm{D}}C}\)
- Xét ΔABD và ΔBDC
Có \(\widehat {AB{\rm{D}}} = \widehat {B{\rm{D}}C}{,^{}}\widehat {DAB} = \widehat {DBC}\)
=> ΔABD ∽ ΔBDC (g.g)
b) Có \(\frac{{AB}}{{B{\rm{D}}}} = \frac{{12}}{{24}} = \frac{1}{2}\)
ΔABD ∽ ΔBDC với tỉ số \(\frac{1}{2}\)
=> \(\frac{3}{{BC}} = \frac{4}{{DC}} = \frac{1}{2}\)
=> BC=6 (cm)
DC=8 (cm)