cho tam giác abc và m là một điểm thuộc miền trong của tam giác đó. gọi d,e,f lần lượt là trung điểm của ab,ac,bc và a',b',c' là điểm đối xứng của M lần lượt qua tâm đối xứng f,e,d
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 1 2018
Gọi I trung điểm LE. Ta có DL//EN//OB và DL = EN = 0.5OB Þ DENL là hình bình hành. Tương tự chứng minh LMEF là hình bình hành. Từ đó suy ra EL,FM, DN đồng quy tại I
CM
25 tháng 7 2019
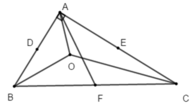
+ Vì O là giao điểm của ba đường phân giác trong tam giác ABC nên O là tâm của đường tròn nội tiếp tam giác ABC nên đáp án A sai.
+ Tam giác ABC vuông tại A có F là trung điểm của BC nên AF là đường trung tuyến ứng với cạnh huyền
Do đó: AF = 1 2 BC (trong tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền)
Suy ra AF = FC = FB
Nên F cách đều ba đỉnh A, B, C
Do đó F là tâm đường tròn ngoại tiếp tam giác ABC.
+ Vì D ≠ E ≠ F và chỉ có một đường tròn ngoại tiếp tam giác ABC nên đáp án B, C sai và D đúng.
Chọn đáp án D
1 tháng 3 2022
a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
AB=AC
\(\widehat{BAE}\) chung
Do đó: ΔABE=ΔACF
b: Ta có: ΔABE=ΔACF
nên BE=CF
Xét ΔFBC vuông tại F và ΔECB vuông tại E có
BC chung
CF=BE
Do đó: ΔFBC=ΔECB
Suy ra: \(\widehat{ICB}=\widehat{IBC}\)
hay ΔIBC cân tại I
c: Ta có: AB=AC
nên A nằm trên đườg trung trực của BC(1)
ta có: IB=IC
nên I nằm trên đường trung trực của BC(2)
Ta có: MB=MC
nên M nằm trên đường trung trực của BC(3)
Từ (1), (2) và (3) suy ra A,I,M thẳng hàng
14 tháng 12 2022
a: Xét ΔCAB có CE/CA=CD/CB
nên ED//AB và ED=AB/2
=>AEDB là hình thang
mà góc EAB=90 độ
nênAEDB là hình thang vuông
b: Xét tứ giác ABKC có
D là trung điểm chung của AK và BC
góc BAC=90 độ
Do đó: ABKC là hình chữ nhật