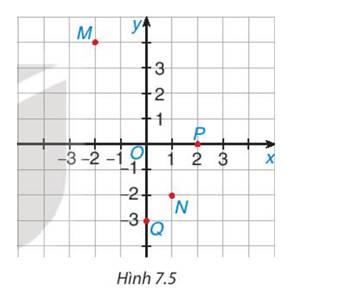
a) Xác định tọa độ của các điểm M,N,P,Q trong Hình 7.5
b) Xác định các điểm R(2; -2) và S(-1; 2) trong Hình 7.5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
25 tháng 8 2023
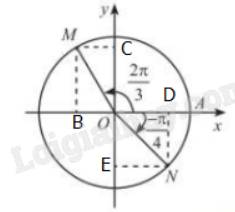
Gọi B, C lần lượt là hình chiếu của M lên Ox, Oy; D, E lần lượt là hình chiếu của N lên Ox, Oy
Ta có: OM = ON = 1
\(\widehat{MOC}=\dfrac{2\pi}{3}-\dfrac{\pi}{2}=\dfrac{\pi}{6}\\ \Rightarrow\left\{{}\begin{matrix}sin\widehat{MOC}=\dfrac{1}{2}\Rightarrow MC=\dfrac{1}{2}\\cos\widehat{MOC}=\dfrac{\sqrt{3}}{2}\Rightarrow MB=\dfrac{\sqrt{3}}{2}\end{matrix}\right.\)
Do điểm M có hoành độ nằm bên trái trục Ox nên tọa độ của điểm M là \(M\left(-\dfrac{1}{2};\dfrac{\sqrt{3}}{2}\right)\)
\(\widehat{NOD}=-\dfrac{\pi}{4}\\ \Rightarrow\left\{{}\begin{matrix}sin\widehat{NOD}=-\dfrac{\sqrt{2}}{2}\Rightarrow ND=-\dfrac{\sqrt{2}}{2}\\cos\widehat{NOD}=\dfrac{\sqrt{2}}{2}\Rightarrow NE=\dfrac{\sqrt{2}}{2}\end{matrix}\right.\)
Vậy tọa độ điểm N là \(N\left(\dfrac{\sqrt{2}}{2};-\dfrac{\sqrt{2}}{2}\right)\)
26 tháng 1 2022
b: A(1;1) B(-2;4)
\(M\left(x;x^2\right)\)
Theo đề, ta có: MA=MB
\(\Leftrightarrow\sqrt{\left(x-1\right)^2+\left(x^2-1\right)^2}=\sqrt{\left(x+2\right)^2+\left(x^2-4\right)^2}\)
\(\Leftrightarrow x^2-2x+1+x^4-2x^2+1=x^2+4x+4+x^4-8x^2+16\)
\(\Leftrightarrow6x^2-6x-18=0\)
\(\Leftrightarrow x^2-x-3=0\)
\(\Delta=\left(-1\right)^2-4\cdot1\cdot\left(-3\right)=13>0\)
Do đó: Phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{1-\sqrt{13}}{2}\\x_2=\dfrac{1+\sqrt{13}}{2}\end{matrix}\right.\)
Vậy: \(M\left(\dfrac{1-\sqrt{13}}{2};\dfrac{7-\sqrt{13}}{2}\right);M\left(\dfrac{1+\sqrt{13}}{2};\dfrac{7+\sqrt{13}}{2}\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2021
Hình chữ nhật ADN gì bạn nhỉ?
Hình chữ nhật phải có 4 đỉnh
KN
2
NV
Nguyễn Việt Dũng
CTVVIP
21 tháng 10 2023
- A (20oB, 20oĐ)
- B (10oĐ, 10oN)
- C (20oT, 10oB)
- D (10oT, 20oN)
- E (30oĐ, 0o)
LA
22 tháng 10 2023
- A (20oB, 20oĐ)
- B (10oĐ, 10oN)
- C (20oT, 10oB)
- D (10oT, 20oN)
- E (30oĐ, 0o)
CM
6 tháng 8 2019
Chứng minh họ đường thẳng y = mx + (2m + 1) (1) luôn đi qua một điểm cố định nào đó.
Giả sử điểm A( x o ; y o ) là điểm mà họ đường thẳng (1) đi qua với mọi m. Khi đó tọa độ điểm A nghiệm đúng phương trình hàm số (1).
Với mọi m, ta có: y o = m x o + (2m + 1) ⇔ ( x o + 2)m + (1 – y) = 0
Vì phương trình nghiệm đúng với mọi giá trị của m nên tất cả các hệ số phải bằng 0.
Suy ra: x o + 2 = 0 ⇔ x o = -2
1 – y o = 0 ⇔ y o = 1
Vậy A(-2; 1) là điểm cố định mà họ đường thẳng y = mx + (2m + 1) luôn đi qua với mọi giá trị m.
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 3 2021
I là trung điểm AC \(\Rightarrow C\left(2;-2\right)\)
\(\Rightarrow\overrightarrow{CM}=\left(2;-1\right)\Rightarrow\) đường thẳng BC có dạng:
\(1\left(x-2\right)+2\left(y+2\right)=0\Leftrightarrow x+2y+2=0\)
Đường thẳng AB qua A và vuông góc BC nên nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình AB:
\(2\left(x+1\right)-1\left(y-2\right)=0\Leftrightarrow2x-y+4=0\)
B là giao điểm AB và BC nên tọa độ là nghiệm:
\(\left\{{}\begin{matrix}x+2y+2=0\\2x-y+4=0\end{matrix}\right.\) \(\Rightarrow B\left(...\right)\)
I là trung điểm BD \(\Rightarrow\left\{{}\begin{matrix}x_D=2x_I-x_B=...\\y_D=2y_I-y_B=...\end{matrix}\right.\)
16 tháng 5 2021
1. \(\overrightarrow{AH}\left(\frac{96}{37};\frac{16}{37}\right)\). AB và CD cùng vuông góc với AH => AB,CD có VTPT cùng phương với vt AH
Đường thẳng AB: đi qua A(1;-2), VTPT (6;1) => \(AB:6\left(x-1\right)+\left(y+2\right)=0\Leftrightarrow6x+y-4=0\)
Đường thẳng CD: đi qua H(133/37;-58/37), VTPT (6;1)
=> \(CD:6\left(x-\frac{133}{37}\right)+\left(y+\frac{58}{37}\right)=0\Leftrightarrow6x+y-20=0\)
2. Xét hệ \(\hept{\begin{cases}2x+y=4\\6x+y=4\end{cases}\Leftrightarrow\hept{\begin{cases}x=0\\y=4\end{cases}\Rightarrow}B\left(0;4\right)}\)
\(\hept{\begin{cases}2x+y=4\\6x+y=20\end{cases}\Leftrightarrow\hept{\begin{cases}x=4\\y=-4\end{cases}\Rightarrow}D\left(4;-4\right)}\)
BD và AC có trung điểm là \(I\left(2;0\right)\), suy ra \(C\left(3;2\right)\).
3. Ta có: \(MA^2+MC^2=2MI^2+\frac{AC^2}{2};MB^2+MD^2=2MI^2+\frac{BD^2}{2}\)
\(\Rightarrow MA^2+MB^2+MC^2+MD^2=4MI^2+\frac{AC^2+BD^2}{2}\ge\frac{AC^2+BD^2}{2}\)(không đổi)
Vậy biểu thức đạt Min khi M trùng với I(3;2).
19 tháng 5 2021
1. →AH(9637 ;1637 ). AB và CD cùng vuông góc với AH => AB,CD có VTPT cùng phương với vt AH
Đường thẳng AB: đi qua A(1;-2), VTPT (6;1) => AB:6(x−1)+(y+2)=0⇔6x+y−4=0
Đường thẳng CD: đi qua H(133/37;-58/37), VTPT (6;1)
=> CD:6(x−13337 )+(y+5837 )=0⇔6x+y−20=0
2. Xét hệ {
| 2x+y=4 |
| 6x+y=4 |
⇔{
| x=0 |
| y=4 |
⇒B(0;4)
{
| 2x+y=4 |
| 6x+y=20 |
⇔{
| x=4 |
| y=−4 |
⇒D(4;−4)
BD và AC có trung điểm là I(2;0), suy ra C(3;2).
3. Ta có: MA2+MC2=2MI2+AC22 ;MB2+MD2=2MI2+BD22
⇒MA2+MB2+MC2+MD2=4MI2+AC2+BD22 ≥AC2+BD22 (không đổi)
Vậy biểu thức đạt Min khi M trùng với I(3;2).
HT
18 tháng 5 2016
đường thẳng AB qua H và vuông HE nên ptdt AB : x+2=0
đường thẳng AD qua K và vuông KE nên ptdt AD : -y+4=0
Tọa độ A là nghiệm của hệ : \(\begin{cases}x+2=0\\-y+4=0\end{cases}\) \(\Leftrightarrow\begin{cases}x=-2\\y=4\end{cases}\) vậy A(-2;4)
\(\overrightarrow{HE}=\left(4;0\right)\Rightarrow HE=AK=4;\overrightarrow{KE}=\left(0;-1\right)\Rightarrow KE=1\) . Vậy \(\overrightarrow{AK}=\frac{4}{5}\overrightarrow{AD}\) , có \(\overrightarrow{AK}=\left(4;0\right);\overrightarrow{AD}=\left(x_D+2;y_D-4\right)\) ta có hê : \(\begin{cases}4=\frac{4}{5}\left(x_D+2\right)\\0=\frac{4}{5}\left(y_D-4\right)\end{cases}\) \(\Leftrightarrow\begin{cases}x=3\\y=4\end{cases}\)Vậy D(3;4)
ptdt DE đi qua D và E nên ta có ptdt: x-y+1=0
Tọa độ điểm B là nghiêm của hệ phương trình đường thẳng DE và AB: \(\begin{cases}x-y=-1\\x=-2\end{cases}\) \(\Leftrightarrow\begin{cases}x=-2\\y=-1\end{cases}\) Vậy B(-2;-1)
Goi O(xo ;yo) là giao điểm của BD và AC. ta có : \(\begin{cases}x_o=\frac{-2+3}{2}=\frac{1}{2}\\y_o=\frac{-1+4}{2}=\frac{3}{2}\end{cases}\) Vậy O(\(\frac{1}{2};\frac{3}{2}\)) . O là trung điểm của AC nên C(3;-1)