so sánh các lũy thừa sau a, 625 mũ 5 và 125 mũ 7 b, 3 mũ 2n và 2 mũ 3n
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NM
Nguyễn Minh Quang
Giáo viên
2 tháng 11 2021
a. \(625^5=\left(5^4\right)^5=5^{20}< 5^{21}=\left(5^3\right)^7=125^7\)
b. với n khác 0 \(3^{2n}=9^n>8^n=2^{3n}\)
Còn với n=0 thì \(3^{2n}=2^{3n}=1\)
TN
7 tháng 10 2017
a, Ta có:\(8^{10}=\left(2^3\right)^{10}=2^{30}\)
\(1024^3=\left(2^{10}\right)^3=2^{30}\)
Vậy \(8^{10}=1024^3\)
b, Dựa theo ý a nhưng cơ số là 5\(\Rightarrow25^7>125^3\)
c, Ta có: \(49^{10}\)giữ nguyên
\(625^5=\left(25^2\right)^5=25^{10}\)
DA
1 tháng 8 2020
a) 273.816
= (33)3. (34)6
= 39.324
= 333
b) 520.12510.6252
= 520.(53)10.(54)2
= 520.530.58
=558
B3: 23+52 và (2+5)2
Ta có: 23 +52= 33
(2+5)2= 100
Vì 33 < 100 nên 23 +52 < (2+5)2
Vậy.........
UN
13
SN
12 tháng 10 2018
a,
15^12=(3*5)^12=3^12*5^12
81^3*125^5=(3^4)^3*(5^3)^5=3^12*5^15
Vì 12<15 suy ra 5^12<5^15
Suy ra 3^12*5^12<3^12*5^15
T
12 tháng 10 2018
\(a.81^3.125^5=\left(3^4\right)^3.\left(5^3\right)^5=3^{12}.5^{15}=3^{12}.5^{12}.5^3=\left(3.5\right)^{12}.5^3=15^{12}.5^3>15^{12}\)
\(b.4^{20}.81^{12}=\left(2^2\right)^{20}.\left(9^2\right)^{12}=2^{40}.9^{24}=2^{20}.2^{20}.9^{20}.9^4=\left(2.9\right)^{20}.2^{20}.9^4=18^{20}.2^{20}.9^4>18^{20}\)
\(c.73^{75}=\left(73^3\right)^{25}=389017^{25}\)
\(107^{50}=107^{2.50}=\left(107^2\right)^{25}=11449^{25}\)
Vì \(389017^{25}>11449^{25}\Rightarrow73^{75}>107^{50}\)
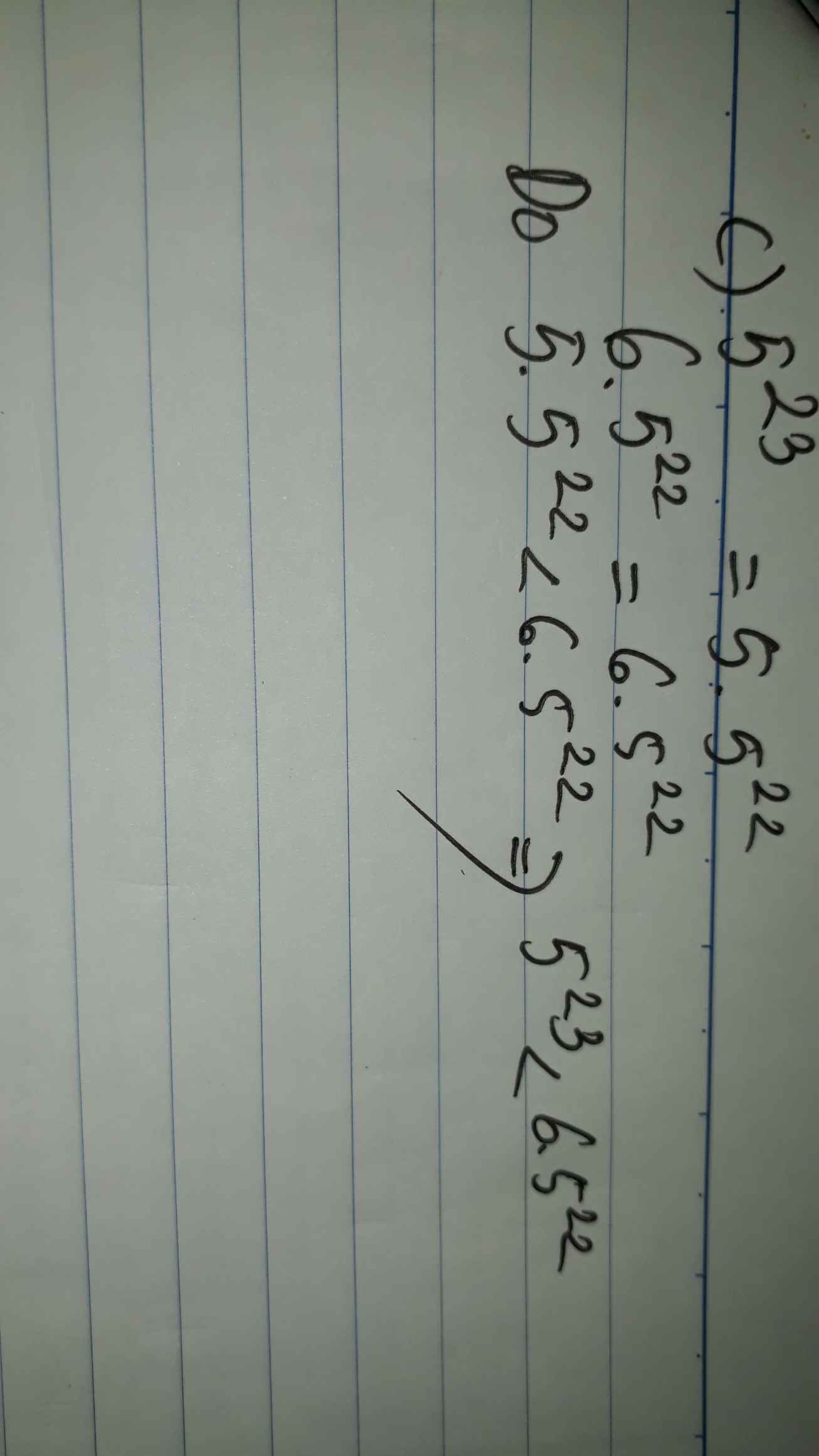
mình đang cần gâps
6255 và 1257
a, 6255 = (54)5 = 520
1257 = (53)7 = 521
Vì 520 < 521 nên 6255 < 1257
b, 32n = (32)n = 9n
23n = (23)n = 8n
9n > 8n ( nếu n > 0)
9n = 8n (nếu n = 0)
Vậy nếu n = 0 thì 23n = 32n
nếu n > 0 thì 32n > 23n