Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


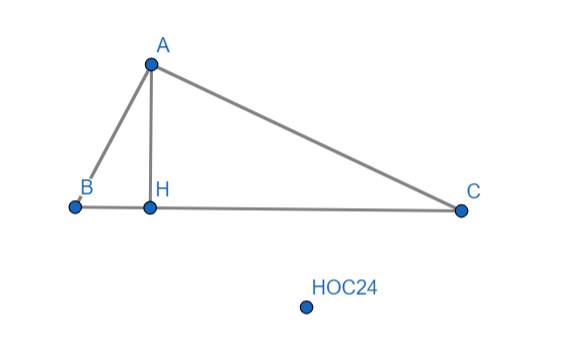
Xét \(\Delta ABC\) và \(\Delta HBA\) có:
\(\widehat{BAC}=\widehat{BHA}=90^o\)
\(\widehat{B}\) chung
\(\Rightarrow\Delta ABC\sim\Delta HBA\left(g.g\right)\) (1)
\(\Rightarrow\dfrac{AB}{BC}=\dfrac{HB}{AB}\) hay \(\dfrac{AB}{4+9}=\dfrac{4}{AB}\Rightarrow AB^2=52\Rightarrow AB=\sqrt{52}=2\sqrt{13}cm\)
Xét \(\Delta\text{A}BC\) và \(\Delta HAC\) có:
\(\widehat{BAC}=\widehat{AHC}=90^o\)
\(\widehat{C}\) chung
\(\Rightarrow\Delta ABC\sim\Delta HAC\left(g.g\right)\) (2)
Từ (1) và (2) \(\Rightarrow\Delta HAB\sim\Delta HCA\)
\(\Rightarrow\dfrac{AH}{HC}=\dfrac{HB}{AH}\) hay \(\dfrac{AH}{9}=\dfrac{4}{AH}\Rightarrow AH^2=36\Rightarrow AH=\sqrt{36}=6\left(cm\right)\)
Ta có \(\Delta ABC\) vuông tại A.
Áp dụng đinh lý Py-ta-go ta có:
\(AC=\sqrt{BC^2-AB^2}=\sqrt{\left(4+9\right)^2-\left(2\sqrt{13}\right)^2}=3\sqrt{13}cm\)
b) Diện tích tam giác ABC là:
\(S_{ABC}=\dfrac{1}{2}\cdot BC\cdot AH=\dfrac{1}{2}\cdot\left(4+9\right)\cdot6=39\left(cm^2\right)\)

1 ,áp dụng bộ 3 pitago trong tam giác abc suy ra AC=5 cm dựa vào pitago đảo có : \(5^2+12^2\)= 13 suy ra tam giác ACD vuông tại c
S tứ giác = SABC +SADC =1/2 .3.4 +1/2. 5.12=36 cm ^2.
2,bài 2 vẽ hình lâu lém tự làm nha bn
3,
B1 minh da lam dc trc do roi nhung van cam on ban vi da giup do

 Tổng số phần của 2 diện tích tam giác :
Tổng số phần của 2 diện tích tam giác :
3 + 2 =5 ( phần )
Diện tích tam giác ACD :
70 : 5 x 3 = 52 ( cm2)
Diện tích tam giác ABC :
70 : 5 x 2 = 28 ( cm2)
Vậy : diện tích tam giác ACD : 52 cm2
______________ ABC : 28 cm2

1.
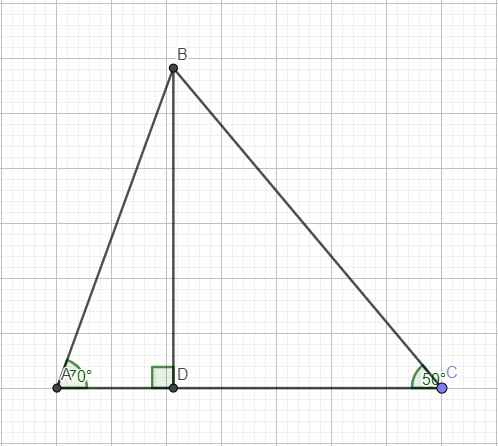
\(A+B+C=180^0\Rightarrow A=180^0-\left(B+C\right)=70^0\)
Kẻ đường cao BD
Trong tam giác vuông ABD:
\(cotA=\dfrac{AD}{BD}\Rightarrow AD=BD.cotA\)
Trong tam giác vuông BCD:
\(cotC=\dfrac{CD}{BD}\Rightarrow CD=BD.cotC\)
\(\Rightarrow AD+CD=BD.cotA+BD.cotC\)
\(\Rightarrow AC=BD.\left(cotA+cotC\right)\)
\(\Rightarrow BD=\dfrac{AC}{cotA+cotC}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}BD.AC=\dfrac{1}{2}.\dfrac{AC^2}{cotA+cotC}=\dfrac{35^2}{2\left(cot70^0+cot50^0\right)}\approx509,1\left(cm^2\right)\)

Chiều cao là:
15 x 2 : 5 = 6 (cm)
Diện tích hình tam giác là:
24 x 6 : 2 = 72 (cm2)
tick cho nhe

\(a,\) Vì M,N là trung điểm AB,BC nên MN là đtb \(\Delta ABC\)
Do đó \(MN//BC\Rightarrow MN//KC\) và \(MN=\dfrac{1}{2}BC=KC\) (K là trung điểm)
Vậy MNCK là hình bình hành
\(b,\) Vì MN là đtb nên \(AC=2MN=10(cm)\)
Áp dụng Pytago: \(HC^2=AC^2-AH^2=6(cm)\)
Vậy \(S_{ACH}=\dfrac{1}{2}AH.HC=\dfrac{1}{2}.6.8=24(cm^2)\)