Bài 1. Cho hình bình hành MNPQ. Kẻ NH vuông góc với MP tại H. Kẻ QK vuông góc với MP tại K. Chứng minh tứ giác NHKQ là hình bình hành
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 10 2021
a: Xét ΔMHQ vuông tại H và ΔPKN vuông tại K có
MQ=PN
\(\widehat{MQH}=\widehat{PNK}\)
Do đó: ΔMHQ=ΔPKN
Suy ra: MH=PK
18 tháng 12 2018
a,b ko khó nên bạn tự giải nha
c)Gọi O la giao điểm của NP và AM
=> O là trung điểm của AM và OM=OA=ON=OP
Xét tam giác AHM vuông tại H
Có O là td của AM (cmt)
=>HO la đường trung tuyến ứng với cạnh huyền AM
=>HO=OA=OM
mà OM=OA=OP=ON (cmt)
=>HO=OP=ON=1/2NP
Xét tam giác NHP
có HO=OP=ON=1/2NP(cmt)
=>tam giác NHP vuông tại H
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
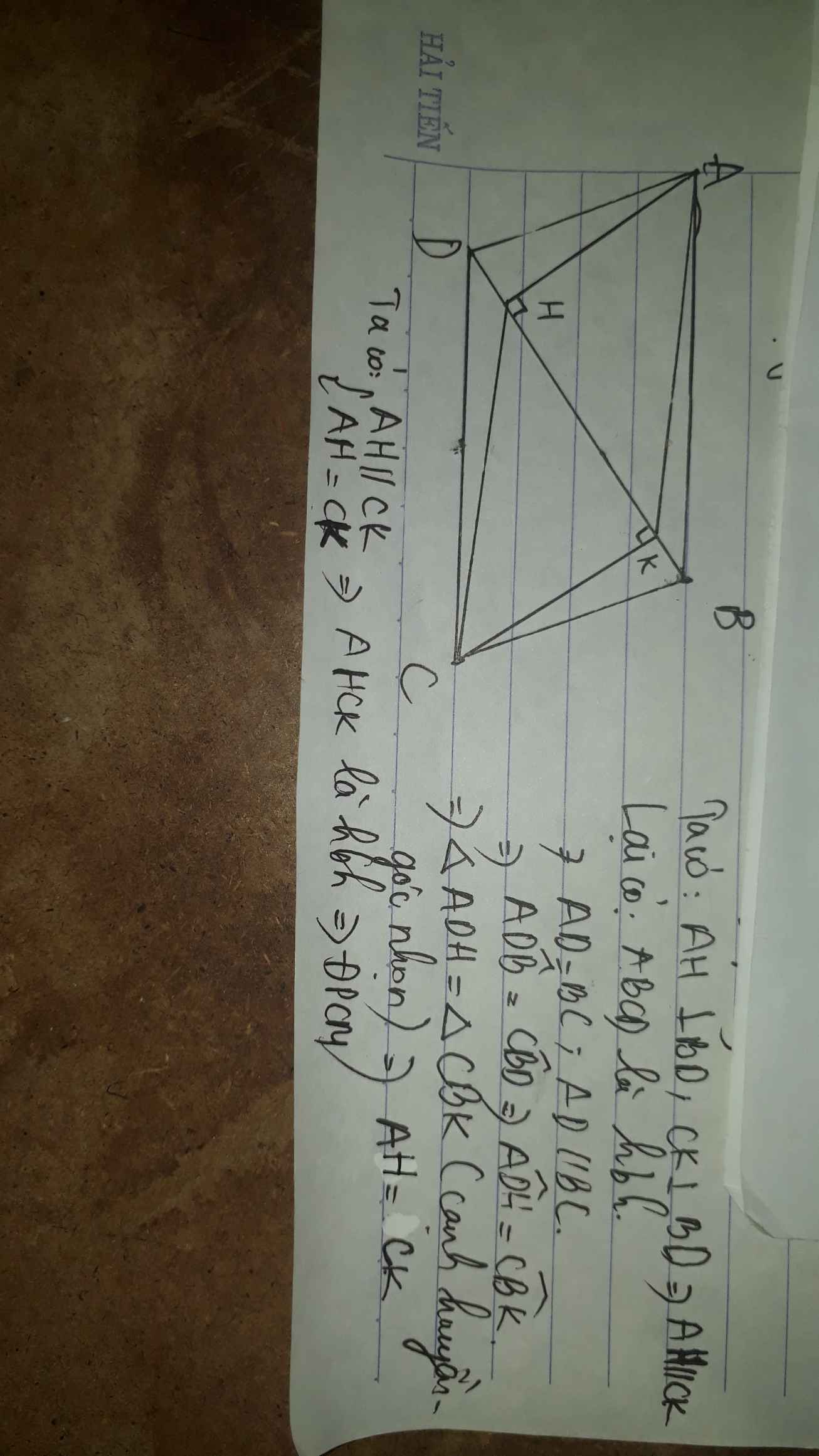
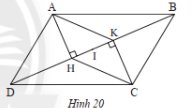
a) Vì \(AH\), \(CK\) vuông góc với \(BD\) (gt)
Suy ra \(AH\) // \(CK\)
Vì \(ABCD\) là hình bình hành (gt)
Suy ra \(AD = BC\); \(AD\) // \(BC\)
Xét \(\Delta ADH\) và \(\Delta CBK\) ta có:
\(\widehat {{\rm{AHD}}} = \widehat {{\rm{CKB}}} = 90^\circ \) (gt)
\(AD = BC\) (cmt)
\(\widehat {{\rm{ADH}}} = \widehat {{\rm{CBK}}}\) (do \(AD\) // \(BC\))
Suy ra \(\Delta ADH = \Delta CBK\) (ch-gn)
Suy ra \(AH = CK\) (hai cạnh tương ứng)
Mà \(AH\) // \(CK\) (cmt)
Suy ra \(AHCK\) là hình bình hành
b) Vì \(AHCK\) là hình bình hành nên hai đường chéo \(HK\) và \(AC\) cắt nhau tại trung điểm.
Mà \(I\) là trung điểm của \(HK\).
Suy ra \(I\) là trung điểm của \(AC\).
Ta lại có \(ABCD\) là hình bình hành nên hai đường chéo \(AC\) và \(BD\) cắt nhau tại trung điểm.
Suy ra \(I\) là trung điểm của \(BD\) hay \( IB = ID\)
23 tháng 2 2023
Xét ΔAHD vuông tại H và ΔAKB vuông tại K có
AH=AK
góc HAD=góc KAB
=>ΔAHD=ΔAKB
=>AD=AB
=>ABCD là hình thoi
Xét \(\Delta\) MQP và \(\Delta\) PNM có:
MP chung; MQ = NP; QP = MN (vì MNPQ là hình bình hành)
⇒ \(\Delta\)MQP = \(\Delta\) PNM ( c-c-c)
⇒ SMQP = SPNM
⇒ QK = HN(1) ( vì hai tam giác có diện tích bằng nhau và chung cạnh đáy thì hai chiều cao tương ứng của hai tam giác đó bằng nhau)
Mặt khác QK \(\perp\) MP
NH \(\perp\) MP
⇒ QH // NH(2) ( vì hai đường thẳng cùng vuông với đường thẳng thứ ba thì hai đường thẳng đó song song với nhau)
Kết hợp (1) và (2) ta có
Tứ giác NHQK là hình bình hành ( vì tứ giác có một cặp cạnh đối diện song song và bằng nhau thì tứ giác đó là hình bình hành)