Hình thang ABCD (AB song song CD) có AB=10, BD=6, MN=4 (M,N là trung điểm AB,CD). Tính \(S_{ABCD}\)
Giari giúp mình với nha mình đang cần gấp lắm. Cảm ơn mn!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
I
Hình thang ABCD (AB song song CD) có AB=10, BD=6, MN= 4 (M,N là trung điểm AB,CD). Tính \(S_{ABCD}\)
0
17 tháng 1 2018
:) à bạn :) nãy mình soạn ra bài đúng r mà nhấn nhầm xoá hết cmnr :))) nên h mình gợi ý thôi nha :(((
bài 1 bạn xét tam giác BCD có NI //CD ( vì MN//CD và I thuộc MN) , =>BN/NC=NI/CD ( hệ quả ...) (1)
xét tam giác ADC r chứng minh tương tự để ra được MK/DC=AM/MD (2)
có AM=BN ( cm ABNM là hbh)
và MD=NC ( cm MNCD là hbh)
=>AM/MD=BN/NC (3)
Từ 1,2,3 => MK/CD=NI/CD
=>MK=CD
=> MI=KN= MK+ KI=NI+KI ( điều phải cm)
17 tháng 1 2018
sorry câu gần cuối ghi sai :))) MK=NI nha bạn
Với đề bài 2 sai thì phải :v bởi nếu trong hình thang ABCD có AB//CD thì AD//BC chứ vậy sao O là giao điểm của hai đường thẳng song song được
7 tháng 2 2020
a, gọi MN cắt BC tại O
xét tam giácBDC có : M là trung điểm của BD (gt)
MO // DC (Gt)
=> O là trung điểm của BC (đl)
xét tam giác ABC có : NO // AB
=> N là trung điểm của AB (đl)
24 tháng 12 2023
Xét ΔADC có MI//DC
nên \(\dfrac{MI}{DC}=\dfrac{AM}{AD}=\dfrac{1}{2}\)
=>\(\dfrac{MI}{12}=\dfrac{1}{2}\)
=>\(MI=6\left(cm\right)\)
Xét hình thang ABCD có
M là trung điểm của AD
MN//AB//CD
Do đó: N là trung điểm của BC
Xét hình thang ABCD có
M,N lần lượt là trung điểm của AD,BC
=>MN là đường trung bình của hình thang ABCD
=>\(MN=\dfrac{AB+CD}{2}=\dfrac{6+12}{2}=\dfrac{18}{2}=9\left(cm\right)\)
DB
23 tháng 5 2017
a/ M là trung điểm AD,N là trung điểm BC .
MN la đường trung bình cua hình thang ABFE
=>MN // AB//DC
=> MA/MD=NB/NC=1/2
b/ Lấy E là trung điểm DM, F là trung điểm NC.
Có EF là đường trung binh hình thang MNCD.
=> EF= (MN+CD)/2
=MN/2 + 17/2
=MN/2+8,5 (1)
MA/MD=1/2
ME/MD=1/2 => MA/AE = 1/2
=> M là trung điểm AE
=> N là trung điểm BF
=> MN là đường trung bình hình thang ABFE
=> MN= (AB+EF)/2
= 8/2 + (MN+8,5)/2
= 4+MN/4+4,25
= 8,25 + MN/4
MN=8,25+MN/4
=> MN-MN/4=8,25
<=> 3MN/4=8,25
<=> 3MN= 8,25 . 4
<=> 3MN=33
<=> MN= 11CM
CM
25 tháng 1 2018
Gọi P là trung điểm của AD. Ta chứng minh được NP và MP lần lượt là đường trung bình của tam giác ABD và ADC nên suy ra NP//AB và MP//DC. Mặt khác AB//CD nên ta có P, N, M thẳng hàng MN//AB//DC
MN
29 tháng 2 2020
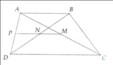
Kẻ AN cắt CD tại E
Xét △ANB và △END có :
^ANB = ^END (đối đỉnh)
NB = ND (gt)
^ABD = ^BDE (so le trong)
\(\Rightarrow\)△ANB = △END (g.c.g)
\(\Rightarrow\)AN = NE (cặp cạnh tương ứng)
Xét △AEC có : AM = MC
AN = NE
\(\Rightarrow\)MN // EC
\(\Rightarrow\)MN // AB // CD (ĐPCM)