Khai triển biểu thức:(2x+3y)2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Trả lời:
a, \(\left(\frac{1}{2}x-3\right)^2=\left(\frac{1}{2}x\right)^2-2.\frac{1}{2}x.3+3^2=\frac{1}{4}x^2-3x+9\)
b, \(\left(2x^2+3y\right)^2=\left(2x^2\right)^2+2.2x^2.3y+\left(3y\right)^2=4x^4+12x^2y+9y^2\)
c, \(\left(3x-7y\right)^2=\left(3x\right)^2-2.3x.7y+\left(7y\right)^2=9x^2-42xy+49y^2\)

Ta có:
\(\begin{array}{l}{\left( {2 - 3y} \right)^4} = {\left[ {2 + \left( { - 3y} \right)} \right]^4} = {2^4} + {4.2^3}.\left( { - 3y} \right) + {6.2^2}.{\left( { - 3y} \right)^2} + {4.2^1}.{\left( { - 3y} \right)^3} + {\left( { - 3y} \right)^4}\\ = 16 - 96y + 216{y^2} - 216{y^3} + 81{y^4}\end{array}\)

a) \({\left( {2x + 1} \right)^4} = {\left( {2x} \right)^4} + 4.{\left( {2x} \right)^3}{.1^1} + 6.{\left( {2x} \right)^2}{.1^2} + 4.\left( {2x} \right){.1^3} + {1^4} = 16{x^4} + 32{x^3} + 24{x^2} + 8x + 1\)
b) \(\begin{array}{l}{\left( {3y - 4} \right)^4} = {\left[ {3y + \left( { - 4} \right)} \right]^4} = {\left( {3y} \right)^4} + 4.{\left( {3y} \right)^3}.\left( { - 4} \right) + 6.{\left( {3y} \right)^2}.{\left( { - 4} \right)^2} + 4.{\left( {3y} \right)^1}{\left( { - 4} \right)^3} + {\left( { - 4} \right)^4}\\ = 81{y^4} - 432{y^3} + 864{y^2} - 768y + 256\end{array}\)
c) \({\left( {x + \frac{1}{2}} \right)^4} = {x^4} + 4.{x^3}.{\left( {\frac{1}{2}} \right)^1} + 6.{x^2}.{\left( {\frac{1}{2}} \right)^2} + 4.x.{\left( {\frac{1}{2}} \right)^3} + {\left( {\frac{1}{2}} \right)^4} = {x^4} + 2{x^3} + \frac{3}{2}{x^2} + \frac{1}{2}x + \frac{1}{{16}}\)
d) \(\begin{array}{l}{\left( {x - \frac{1}{3}} \right)^4} = {\left[ {x + \left( { - \frac{1}{3}} \right)} \right]^4} = {x^4} + 4.{x^3}.{\left( { - \frac{1}{3}} \right)^1} + 6.{x^2}.{\left( { - \frac{1}{3}} \right)^2} + 4.x.{\left( { - \frac{1}{3}} \right)^3} + {\left( { - \frac{1}{3}} \right)^4}\\ = {x^4} - \frac{4}{3}{x^3} + \frac{2}{3}{x^2} - \frac{4}{27}x + \frac{1}{{81}}\end{array}\)

\(A=\left(2x-3y\right)\left(5x-2y\right)=10x^2-4xy-15xy+6y^2=10x^2-19xy+6y^2\)

a) \(\left(2x^2-1\right)^2\)
\(=4x^4-4x^2+1\)
b)\(\left(\dfrac{1}{2}x+3y^2\right)^2\)
\(=\dfrac{1}{4}x^2+3xy^2+9y^4\)

\(\left(2x-3y\right)^{10}\)
\(=\left(2x\right)^{10}-C^1_{10}\cdot\left(2x\right)^9\cdot3y+C^2_{10}\cdot\left(2x\right)^8\cdot\left(3y\right)^2+...+\left(3y\right)^{10}\)
\(=1024x^{10}-1536x^9y+...+59049y^{10}\)

a) \(\left(2x^2-1\right)^2=\left(2x^2\right)^2-2.2x^2.1+1^2\)
\(=4x^4-4x^2+1\).
b) \(\left(\frac{1}{2}x+3y^2\right)^2=\left(\frac{1}{2}x\right)^2+2.\frac{1}{2}x.3y^2+\left(3y^2\right)^2\)
\(=\frac{1}{4}x^2+3y^2x+9y^4\)
Chúc bn hc tốt!
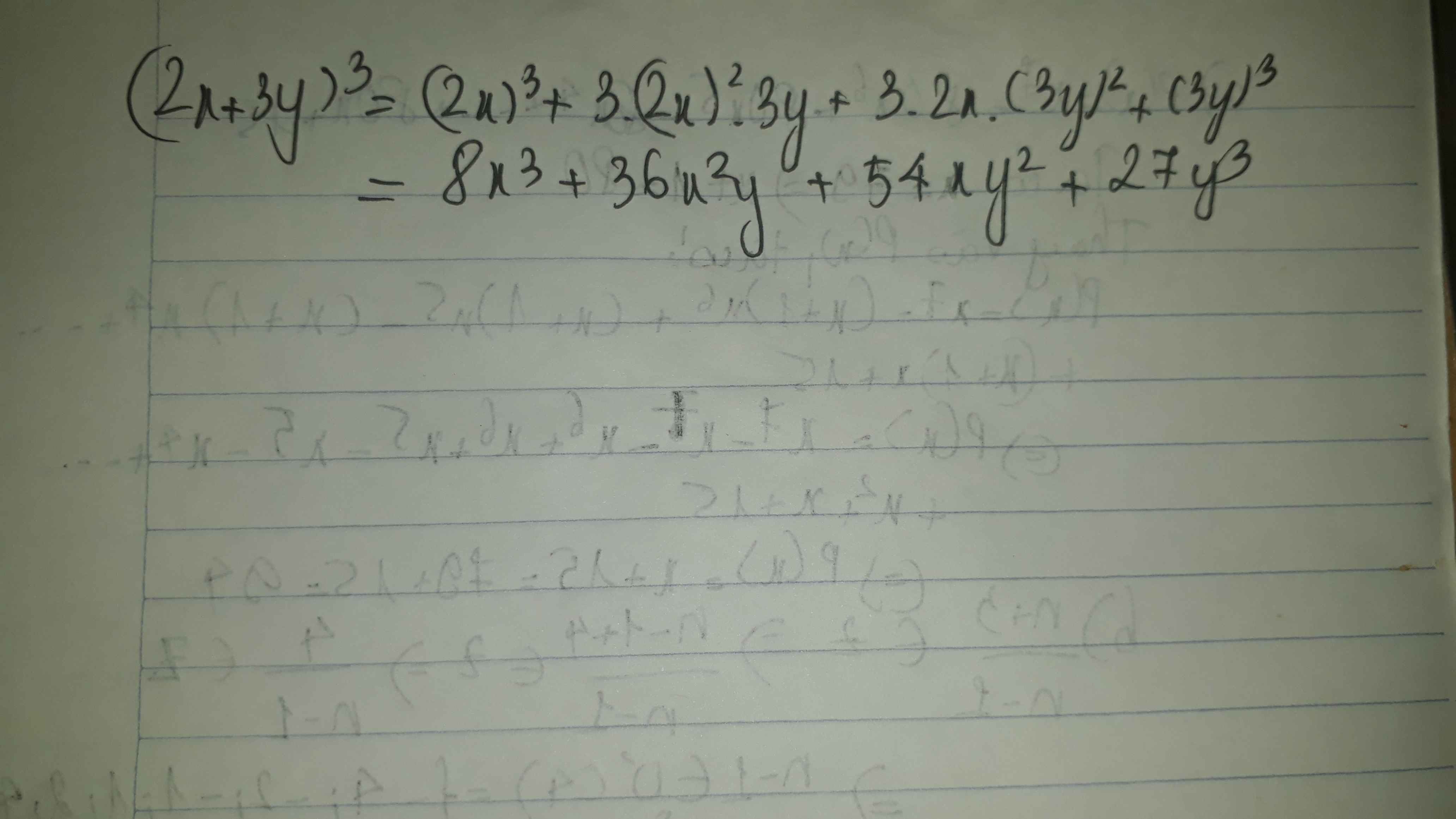
(2\(x\) + 3y)2
= (2\(x\) + 3y).(2\(x\) + 3y)
= 4\(x\)2 + 6\(xy\) + 6\(xy\) + 9y2
= 4\(x^2\) + 12\(xy\) + 9y2
\(4x^2+12xy+9y^2\)