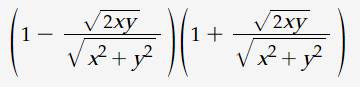
Tìm đk , rút gọn và tính P khi a = b
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
15 tháng 9 2023
Lời giải:
ĐKXĐ: $x>0; x\neq 1; x\neq 9$
\(A=\frac{1}{\sqrt{x}(\sqrt{x}-1)}:\frac{(\sqrt{x}+1)(\sqrt{x}-1)+(\sqrt{x}+3)(\sqrt{x}-3)}{(\sqrt{x}-3)(\sqrt{x}-1)}\)
\(=\frac{1}{\sqrt{x}(\sqrt{x}-1)}:\frac{x-1-(x-9)}{(\sqrt{x}-3)(\sqrt{x}-1)}=\frac{1}{\sqrt{x}(\sqrt{x}-1)}:\frac{8}{(\sqrt{x}-1)(\sqrt{x}-3)}\)
\(=\frac{1}{\sqrt{x}(\sqrt{x}-1)}.\frac{(\sqrt{x}-1)(\sqrt{x}-3)}{8}=\frac{\sqrt{x}-3}{8\sqrt{x}}\)
Để $A<0\Leftrightarrow \frac{\sqrt{x}-3}{8\sqrt{x}}<0$
$\Leftrightarrow \sqrt{x}-3<0$ (do $8\sqrt{x}>0$)
$\Leftrightarrow \sqrt{x}<3$
$\Leftrightarrow 0\leq x< 9$
Kết hợp với đkxđ suy ra $0< x< 9; x\neq 1$
Khi $x=3-2\sqrt{2}=(\sqrt{2}-1)^2$
$\Rightarrow \sqrt{x}=\sqrt{2}-1$
Khi đó: $A=\frac{\sqrt{x}-3}{8\sqrt{x}}=\frac{\sqrt{2}-4}{8(\sqrt{2}-1)}=\frac{-2-3\sqrt{2}}{8}$
15 tháng 9 2023
sao chỗ x−1−(x−9) lại là trừ ạ đáng lẽ nó phải là (x−1)+(x−9) chứ ạ
VT
1
H9
HT.Phong (9A5)
CTVHS
15 tháng 9 2023
\(\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{1}{\sqrt{x}}\right):\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-3}+\dfrac{\sqrt{x}+3}{\sqrt{x}-1}\right)\) (ĐK: \(x>0;x\ne1;x\ne9\))
\(=\left[\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{\sqrt{x}-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right]:\left[\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)}+\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)}\right]\)
\(=\dfrac{\sqrt{x}-\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{x-1+x-9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{2x-10}{\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-1\right)}{2\left(x-5\right)}\)
\(=\dfrac{\sqrt{x}-3}{2\sqrt{x}\left(x-5\right)}\)
\(=\dfrac{\sqrt{x}-3}{2x\sqrt{x}-10\sqrt{x}}\)
\(A>0\) khi
\(\dfrac{\sqrt{x}-3}{2x\sqrt{x}-10\sqrt{x}}>0\)
TH1:
\(\sqrt{x}-3>0\) và \(2x\sqrt{x}-10\sqrt{x}>0\)
\(\Leftrightarrow\sqrt{x}>3\) và \(2\sqrt{x}\left(x-5\right)>0\)
\(\Leftrightarrow x>9\) và \(x>5\)
\(\Leftrightarrow x>9\)
TH2:
\(\sqrt{x}-3< 0\) và \(2x\sqrt{x}-10\sqrt{x}< 0\)
\(\Leftrightarrow\sqrt{x}< 3\) và \(2\sqrt{x}\left(x-5\right)< 0\)
\(\Leftrightarrow x< 9\) và \(x< 5\)
\(\Leftrightarrow x< 5\)
Vậy A > 0 khi \(\left[{}\begin{matrix}x>9\\x< 5\end{matrix}\right.\)
Ta có:
\(x=3-2\sqrt{2}=\left(\sqrt{2}\right)^2-2\cdot\sqrt{2}\cdot1+1^2=\left(\sqrt{2}-1\right)^2\)
\(A=\dfrac{\sqrt{\left(\sqrt{2}-1\right)^2}-3}{2\cdot\left(\sqrt{2}-1\right)^2\cdot\sqrt{\left(\sqrt{2}-1\right)^2}-10\cdot\sqrt{\left(\sqrt{2}-1\right)^2}}\)
\(A=\dfrac{\left|\sqrt{2}-1\right|-3}{2\cdot\left(3-2\sqrt{2}\right)\cdot\left|\sqrt{2}-1\right|-10\cdot\left|\sqrt{2}-1\right|}\)
\(A=\dfrac{\sqrt{2}-1-3}{\left(6-4\sqrt{2}\right)\left(\sqrt{2}-1\right)-10\left(\sqrt{2}-1\right)}\)
\(A=\dfrac{\sqrt{2}-4}{6\sqrt{2}-6-8+4\sqrt{2}-10\sqrt{2}+10}\)
\(A=\dfrac{\sqrt{2}-4}{-4}\)
\(A=\dfrac{4-\sqrt{2}}{4}\)
HK
0
23 tháng 12 2020
a) Điều kiện: \(x\ne\pm1\)
\(B=\frac{x-1}{x+1}-\frac{x+1}{x-1}-\frac{4}{1-x^2}\)
\(B=\frac{\left(x-1\right).\left(x-1\right)}{\left(x+1\right).\left(x-1\right)}-\frac{\left(x+1\right).\left(x+1\right)}{\left(x-1\right).\left(x+1\right)}-\frac{-4}{\left(x-1\right).\left(x+1\right)}\)
\(B=\frac{x^2-x-x+1-x^2-x-x-1+4}{\left(x-1\right).\left(x+1\right)}\)
\(B=\frac{-4x+4}{\left(x-1\right).\left(x+1\right)}=\frac{-4.\left(x-1\right)}{\left(x-1\right).\left(x+1\right)}=\frac{-4}{x+1}\)
b) \(x^2-x=0\Leftrightarrow x.\left(x-1\right)=0\Leftrightarrow\orbr{\begin{cases}x=0\\x=1\end{cases}}\)
Khi \(x=0\Leftrightarrow\frac{-4}{0-1}=\frac{-4}{-1}=4\)
Khi \(x=1\Leftrightarrow\frac{-4}{1-1}=0\)
c) \(\frac{-4}{x+1}=-3\Leftrightarrow-3.\left(x+1\right)=-4\Leftrightarrow x+1=\frac{4}{3}\Leftrightarrow x=\frac{1}{3}\)
30 tháng 8 2023
ĐKXĐ: x>0 và y>0
Sửa đề: \(A=\left(x-\dfrac{\sqrt{xy^2}+y\sqrt{y}}{\sqrt{x}+\sqrt{y}}\right)\left(\dfrac{\sqrt{y}}{\sqrt{xy}+y}-\dfrac{\sqrt{x}}{\sqrt{xy}-x}+\dfrac{\sqrt{y}}{x-y}\right)\)
\(=\left(x-\dfrac{y\left(\sqrt{x}+\sqrt{y}\right)}{\sqrt{x}+\sqrt{y}}\right)\left(\dfrac{\sqrt{y}}{\sqrt{y}\left(\sqrt{x}+\sqrt{y}\right)}-\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{y}-\sqrt{x}\right)}+\dfrac{\sqrt{y}}{x-y}\right)\)
\(=\left(x-y\right)\cdot\left(\dfrac{1}{\sqrt{x}+\sqrt{y}}+\dfrac{1}{\sqrt{x}-\sqrt{y}}+\dfrac{\sqrt{y}}{x-y}\right)\)
\(=\left(x-y\right)\cdot\dfrac{\sqrt{x}-\sqrt{y}+\sqrt{x}+\sqrt{y}+\sqrt{y}}{x-y}\)
\(=2\sqrt{x}+\sqrt{y}\)
1 tháng 1 2022
a: Thay x=16 vào A, ta được:
\(A=\dfrac{2\cdot4}{4+3}=\dfrac{8}{7}\)
TG
0
23 tháng 5 2019
\(A=\frac{1}{\sqrt{x-1}-\sqrt{x}}+\frac{1}{\sqrt{x-1}+\sqrt{x}}+\frac{\sqrt{x^3}-x}{\sqrt{x}-1}\) \(ĐKXĐ:x\ne\pm1\)
\(=\frac{\sqrt{x-1}+\sqrt{x}+\sqrt{x-1}-\sqrt{x}}{\left(\sqrt{x-1}-\sqrt{x}\right)\left(\sqrt{x-1}+\sqrt{x}\right)}+\frac{x\sqrt{x}-x}{\sqrt{x}-1}\)
\(=\frac{2\sqrt{x-1}}{x-1-x}+\frac{x\left(\sqrt{x}-1\right)}{\sqrt{x}-1}\)
\(=x-2\sqrt{x-1}\)
Câu c mình ko làm được
Sửa đề: a = b => x = y
\(P=\left(1-\dfrac{\sqrt{2xy}}{\sqrt{x^2+y^2}}\right)\left(1+\dfrac{\sqrt{2xy}}{\sqrt{x^2+y^2}}\right)\) (ĐK: \(x,y>0\))
\(=1-\left(\dfrac{\sqrt{2xy}}{\sqrt{x^2+y^2}}\right)^2\)
\(=1-\dfrac{\left(\sqrt{2xy}\right)^2}{\left(\sqrt{x^2+y^2}\right)^2}\)
\(=1-\dfrac{2xy}{x^2+y^2}\)
\(=\dfrac{x^2+y^2-2xy}{x^2+y^2}\)
\(=\dfrac{\left(x-y\right)^2}{x^2+y^2}\)
Khi x = y, ta được: \(P=\dfrac{\left(x-y\right)^2}{x^2+y^2}=\dfrac{\left(x-x\right)^2}{x^2+y^2}=0\)
#Urushi