Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a. Xét tam giác ABM và tam giác DCM có:
+, BM = MC ( AM là đường trung tuyến của tam giác ABC )
+, Góc AMB = góc DMC ( 2 góc đối đỉnh )
+, AM = MD ( gt )
=> tam giác ABM = tam giác DCM ( c.g.c )
=> AB = CD ( 2 cạnh tương ứng )
=> góc BAM = góc CDM ( 2 góc tương ứng )
Mà 2 góc này ở vị trí so le trong
=> AB // CD ( đpcm )
Mình làm câu đầu tiên nhé :)
a) Xét tam giác ABM và tam giác DMC có :
BM = CM ( gt )
\(\widehat{AMB}=\widehat{DMC}\)
AM = DM ( gt )
\(\Rightarrow\)\(\Delta AMB=\Delta DMC\left(c-g-c\right)\)
\(\Rightarrow\)\(\widehat{BAM}=\widehat{DCM}\)( 2 góc tương ứng bằng nhau )
Mà 2 góc này ở vị trí so le trong nên suy ra AB // CD
a.
Xét \(\Delta AMB\) và \(\Delta DMC\) ; có :
\(MA=MD\left(gt\right)\\ \widehat{AMB}=\widehat{DMC}\left(đ^2\right)\\ MB=MC\\ \Rightarrow\Delta AMB=\Delta DMC\left(c-g-c\right)\\ \Rightarrow AB=CD;\widehat{MAB}=\widehat{MDC}\\ \widehat{MAB}=\widehat{MDC}\)
=> AB // CD
TT : AC// BD ; AC=BD
b.
Có vấn đề chỗ BF cắt BC tại K ; !!
coi lại đề
a. Xét tam giác ABM và tam giác DCM có:
+, BM = MC ( AM là đường trung tuyến của tam giác ABC )
+, Góc AMB = góc DMC ( 2 góc đối đỉnh )
+, AM = MD ( gt )
=> tam giác ABM = tam giác DCM ( c.g.c )
=> AB = CD ( 2 cạnh tương ứng )
=> góc BAM = góc CDM ( 2 góc tương ứng )
Mà 2 góc này ở vị trí so le trong
=> AB // CD ( đpcm )
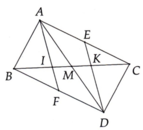
a: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
Do đó:ABDC là hình bình hành
=>AB//CD và AB=CD
b: Xét ΔABD có
AF,BM là trung tuyến
AF cắt BM tại I
=>I là trọng tâm
=>BI=2/3BM=2/3*1/2BC=1/3BC
Xét ΔACD có
DE,CM là trung tuyến
DE cắt CM tại K
Do đó: K là trọng tâm
=>CK=2/3CM=2/3*1/2*BC=1/3BC
c: BI+IK+KC=BC
=>1/3BC+IK+1/3BC=BC
=>IK=1/3BC
=>BI=IK=KC
d: Xét tứ giác AEDF có
AE//DF
AE=DF
Do đó: AEDF là hình bình hành
=>AD cắt EF tại trung điểm của mỗi đường
=>E,M,F thẳng hàng