1) cho hình chóp S.ABCD đáy ABCD là hình bình hành. Xét vị trí của AB và CD
2) cho hình chóp S.ABCD đáy ABCD là hình vuông
a) xét vị trí của AD và BC
b) tìm giao điểm của 2 mặt phẳng (SAB) và (SCD)
c) tìm giao tuyến của 2 mặt phẳng (SAB) và (SCD)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a:
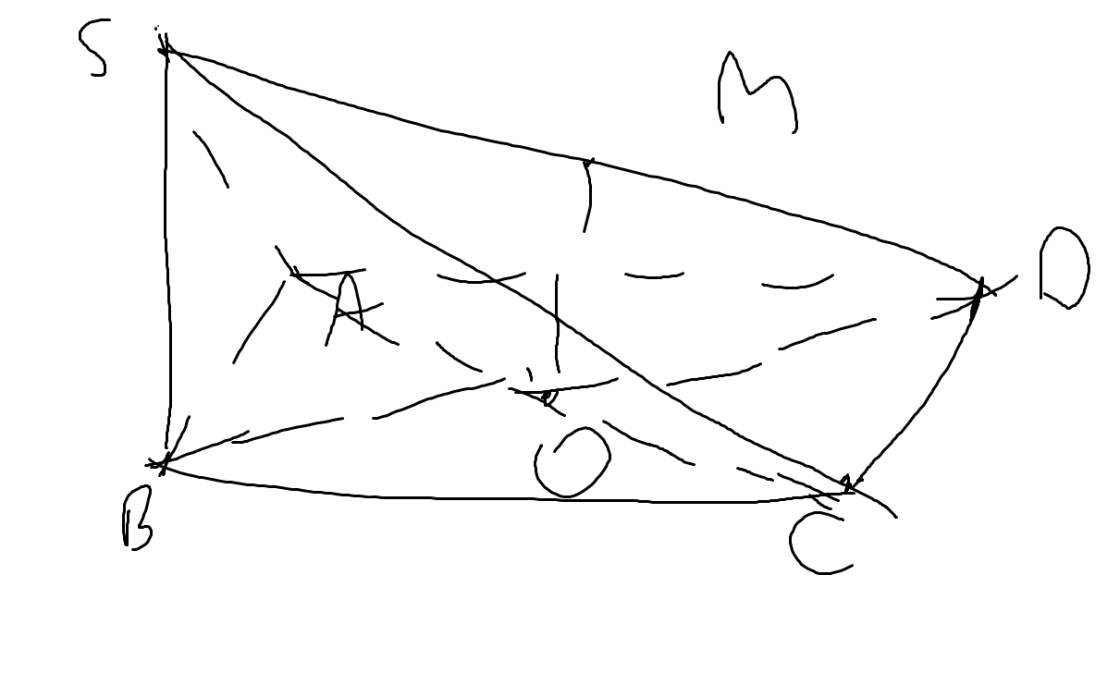
b: \(O\in BD\subset\left(SBD\right);M\in SD\subset\left(SBD\right)\)
=>\(OM\subset\left(SBD\right)\)
c: Xét ΔDSB có
O,M lần lượt là trung điểm của DB,DS
=>OM là đường trung bình của ΔSDB
=>OM//SB
OM//SB
\(SB\subset\left(SBA\right)\)
OM không nằm trong mp(SBA)
Do đó: OM//(SBA)
d: OM//SB
\(SB\subset\left(SBC\right)\)
OM không nằm trong(SBC)
Do đó: OM//(SBC)
e: SB//MO
\(MO\subset\left(MAC\right)\)
SB không nằm trong mp(AMC)
Do đó: SB//(MAC)
f: Xét (OMA) và (SAB) có
\(A\in\left(OMA\right)\cap\left(SAB\right)\)
OM//SB
Do đó: (OMA) giao (SAB)=xy, xy đi qua A và xy//OM//SB

a: \(C\in AI\)
\(C\in BC\)
Do đó: AI cắt BC tại C
b: HK thuộc mp(SBD)
BC thuộc mp(SBC)
Do đó: HK và BC là hai đường chéo nhau
c:Trong mp(SBD), ta có: HK và SI không song song
=>HK cắt SI tại M
d: \(H\in BC\subset\left(SBC\right)\)
\(H\in AH\)
Do đó: AH cắt (SBC)=H

a: Xét ΔSBC có M,N lần lượt là trung điểm của SB,SC
=>MN là đường trung bình
=>MN//BC
b: MN//BC
BC//AD
Do đó: MN//AD
c: \(C\in SN;C\in CD\)
Do đó: SN cắt CD tại C
d: B thuộc SM
B thuộc BC
Do đó: SM cắt BC tại B
e: MN thuộc mp(SBC)
AB thuộc mp(SAB)
Do đó: MN và AB là hai đường chéo nhau
f: \(I\in SI;I\in\left(ABCD\right)\)
Do đó: \(SI\cap\left(ABCD\right)=I\)

a) S là điểm chung của hai mặt phẳng (SAB) và (SCD) mà AB // CD
Từ S kẻ Sx sao cho Sx // AB // CD nên Sx là giao tuyến của hai mặt phẳng (SAB) và (SCD).
b) Gọi E là trung điểm của AB
G là trọng tâm tam giác SAB nên \(\frac{{EG}}{{SE}} = \frac{1}{3}\)
N là trọng tâm tam giác ABC nên\(\frac{{EN}}{{EC}} = \frac{1}{3}\)
Theo Ta lét, suy ra GN // SC mà SC \( \subset \) (SAC). Do đó, GN // (SAC)

a: 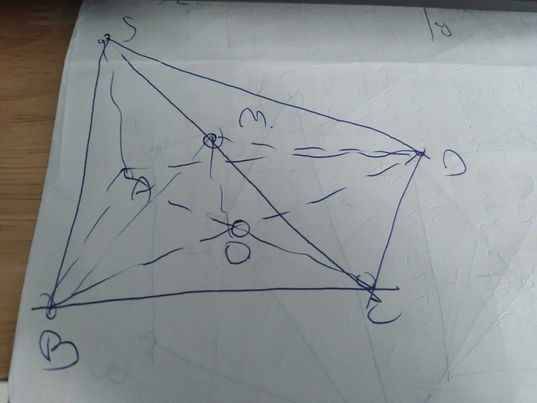
b: \(O\in AC\subset\left(SAC\right);M\in SC\subset\left(SAC\right)\)
Do đó: \(OM\subset\left(SAC\right)\)
c: Xét ΔCAS có
O,M lần lượt là trung điểm của CA,CS
=>OM là đường trung bình
=>OM//SA và OM=SA/2
OM//SA
\(SA\subset\left(SAD\right)\)
OM không nằm trong mp(SAD)
Do đó: OM//(SAD)
d: SA//MO
\(MO\subset\left(MBD\right)\)
SA không nằm trong mp(MBD)
Do đó: SA//(MBD)
e: Xét (OMD) và (SAD) có
OM//SA
\(D\in\left(OMD\right)\cap\left(SAD\right)\)
Do đó: (OMD) giao (SAD)=xy, xy đi qua D và xy//OM//SA

a:
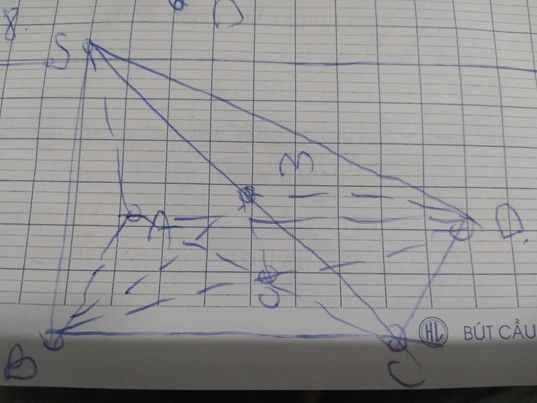
b: \(O\in AC\subset\left(SAC\right)\)
\(M\in SC\subset\left(SAC\right)\)
Do đó: \(OM\subset\left(SAC\right)\)
c: Xét ΔSAC có
O,M lần lượt là trung điểm của CA,CS
=>OM là đường trung bình của ΔSAC
=>OM//SA và \(OM=\dfrac{1}{2}SA\)
OM//SA
SA\(\subset\left(SAD\right)\)
OM không thuộc mp(SAD)
Do đó: OM//(SAD)
d: SA//MO
\(MO\subset\left(MBD\right)\)
SA không thuộc mp(MBD)
Do đó: SA//(MBD)
e: Xét (OMD) và (SAD) có
\(D\in\left(OMD\right)\cap\left(SAD\right)\)
OM//SA
Do đó: \(\left(OMD\right)\cap\left(SAD\right)=xy,D\in xy\) và xy//OM//SA

a: 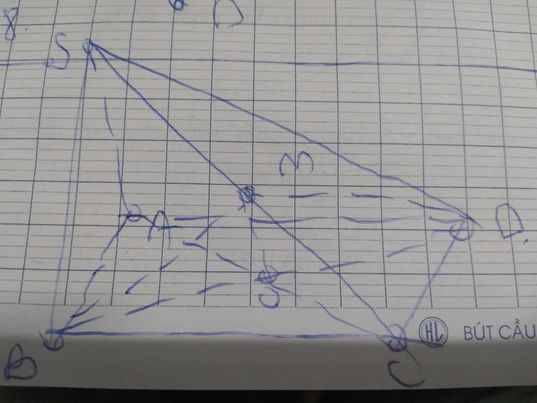
b: \(O\in AC\subset\left(SAC\right)\)
\(M\in SC\subset\left(SAC\right)\)
Do đó: \(OM\subset\left(SAC\right)\)
c: Xét ΔSAC có
O,M lần lượt là trung điểm của CA,CS
=>OM là đường trung bình của ΔSAC
=>OM//SA và \(OM=\dfrac{1}{2}SA\)
OM//SA
SA\(\subset\left(SAD\right)\)
OM không thuộc mp(SAD)
Do đó: OM//(SAD)
d: SA//MO
\(MO\subset\left(MBD\right)\)
SA không thuộc mp(MBD)
Do đó: SA//(MBD)
e: Xét (OMD) và (SAD) có
\(D\in\left(OMD\right)\cap\left(SAD\right)\)
OM//SA
Do đó: \(\left(OMD\right)\cap\left(SAD\right)=xy,D\in xy\) và xy//OM//SA
2:
a: AD và BC là hai đường thẳng song song
b: \(S\in\left(SAB\right)\)
\(S\in\left(SCD\right)\)
Do đó:S là giao điểm của hai mặt phẳng (SAB) và (SCD)
c: AB//CD
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
Do đó; \(\left(SAB\right)\cap\left(SCD\right)=mn\), mn đi qua S và mn//AB//CD