tìm các hệ số a,b để đa thúc:
P= 2x3 -3x2 +ã+b chia cho x-1 dư 15 , chia cho x+2 dư -18
cứu mik với sắp muộn mất rồi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
25 tháng 8 2023
Đúng(2)
Những câu hỏi liên quan
NT
0
CM
24 tháng 2 2018
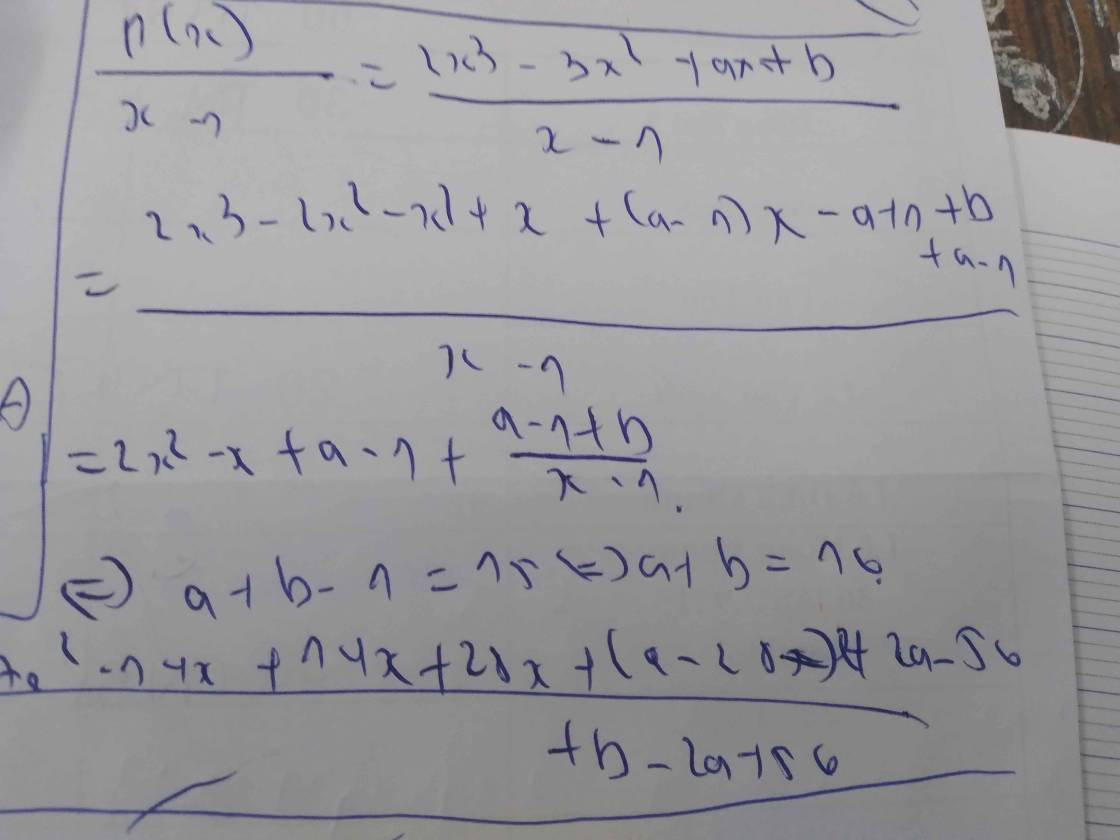
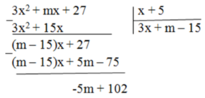
A(x) chia cho B(x) có số dư bằng 2 nên 102 – 5m = 2 ⇒ -5m = 100
⇒ m = 20
PT
1
CM
28 tháng 4 2017
Thực hiện phép chia:
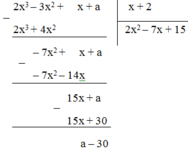
2x3 – 3x2 + x + a chia hết cho x + 2
⇔ số dư = a – 30 = 0
⇔ a = 30.
Cách 2: Phân tích 2x3 – 3x2 + x + a thành nhân tử có chứa x + 2.
2x3 – 3x2 + x + a
= 2x3 + 4x2 – 7x2 – 14x + 15x + 30 + a – 30
(Tách -3x2 = 4x2 – 7x2; x = -14x + 15x)
= 2x2(x + 2) – 7x(x + 2) + 15(x + 2) + a – 30
= (2x2 – 7x + 15)(x + 2) + a – 30
2x3 – 3x2 + x + a chia hết cho x + 2 ⇔ a – 30 = 0 ⇔ a = 30.
HG
3
A
5 tháng 8 2023
Số dư của phép chia đa thức \(\text{f( x ) = 2x^3 - 3x^2 + x + a}\) cho \(\text{x + 2}\) là
\(\text{f ( -2 ) = 2(-2) ^3 - 3 (-2 )^2 + ( - 2 ) + a = -30 + a}\)
Để phép chia là chia hết thì số dư bằng \(\text{0}\)
Hay \(\text{-30 + a = 0}\) \(\Rightarrow\) \(\text{a = 30}\)
VT
2
KT
9 tháng 5 2018
Đa thức \(f\left(x\right)=2x^3-3x^2+x+a\) chia hết cho đa thức \(x+2\)
\(\Leftrightarrow\)\(f\left(-2\right)=0\)
\(\Leftrightarrow\)\(2.\left(-2\right)^3-3.\left(-2\right)^2+\left(-2\right)+a=0\)
\(\Leftrightarrow\)\(-30+a=0\)
\(\Leftrightarrow\)\(a=30\)
Vậy \(a=30\)thì \(2x^3-3x^2+x+a\)chia hết cho \(x+2\)
p/s: bn có thế lm theo cách truyền thống: đặt tính chia ra rồi đặt dư = 0 và tìm a
hoặc dùng hệ số bất định
9 tháng 5 2018
2x^3-3x^2+x+a | x+2
------------------|-------------
2x^3-3x^2 | 2x^2-7x+15
2x^2+4x^2
-7x^2+x
-7x^2-14x
15x+a
15x+30
\(2x^3-3x^2+x+a\div x+2\)
Để đa thức \(2x^3+3x^2+x+a⋮x+2\)
\(\Rightarrow15x+a=15x+30\)
\(\Rightarrow a-30=0\Rightarrow a=30\)
TY
3
9 tháng 3 2016
Ban co the bi sai de nhe aban oi dung phai la x^2+ax-15 moi dung chu
4 tháng 10 2023
2) Ta có đẳng thức sau: \(\left(a+b\right)\left(b+c\right)\left(c+a\right)=\left(a+b+c\right)\left(ab+bc+ca\right)-abc\)
Chứng minh thì bạn chỉ cần bung 2 vế ra là được.
\(\Rightarrow P=\left(a+b+c\right)\left(ab+bc+ca\right)-2abc\)
Do \(a+b+c⋮4\) nên ta chỉ cần chứng minh \(abc⋮2\) là xong. Thật vậy, nếu cả 3 số a, b,c đều không chia hết cho 2 thì \(a+b+c\) lẻ, vô lí vì \(a+b+c⋮4\). Do đó 1 trong 3 số a, b, c phải chia hết cho 2, suy ra \(abc⋮2\).
Do đó \(P⋮4\)