Bài 2: Cho △ABC vuông tại A. Lấy điểm M thuộc cạnh BC. Kẻ MD và ME lần lượt vuông góc với AB và AC ( D thuộc AB, E thuộc AC ). Lấy I là trung điểm của DE.
a) Tứ giác ADME là hình gì? Vì sao?
b) Chứng minh ba điểm A, I, M thẳng hàng.
c) Trên tia đối của tia DM lấy điểm P, trên tia đối của tia EM lấy điểm Q sao cho, DP=DM, EQ=EM
Chứng minh A, P, Q thẳng hàng và A là trung điểm PQ
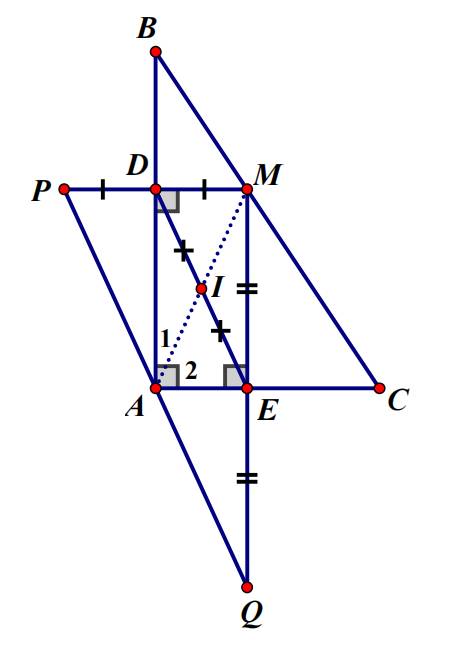



a: Xét tứ giác ADME có
góc ADM=góc AEM=góc DAE=90 độ
Do đó: ADME là hình chữ nhật
b:ADME là hình chữ nhật
=>AM cắt DE tại trung điểm của mỗi đường
mà I là trung điểm của DE
nên I là trung điểm của AM
=>A,I,M thẳng hàng
c: Xét ΔAMQ có
AE vừa là đường cao, vừa là trung tuyến
=>ΔAMQ cân tại A
=>AE là phân giác của góc MAQ(1)
Xét ΔAMP có
AD vừa là đường cao, vừa là trung tuyến
=>ΔAMP cân tại A
=>AD là phân giác của góc MAP(2)
Từ (1), (2) suy ra góc PAQ=góc MAP+góc MAQ
=2(góc BAM+góc CAM)
=2*góc BAC
=180 độ
=>P,A,Q thẳng hàng
mà AP=AQ=AM
nên A là trung điểm của PQ