bài 2: cho hình vẽ, biết góc aAc = 140 độ, góc ABd= 40 độ
a) c/m Ac//Bd
b) gọi Am là p/g góc cAB
Gọi Bm là p/g góc ABd
c) c/m An//Bm
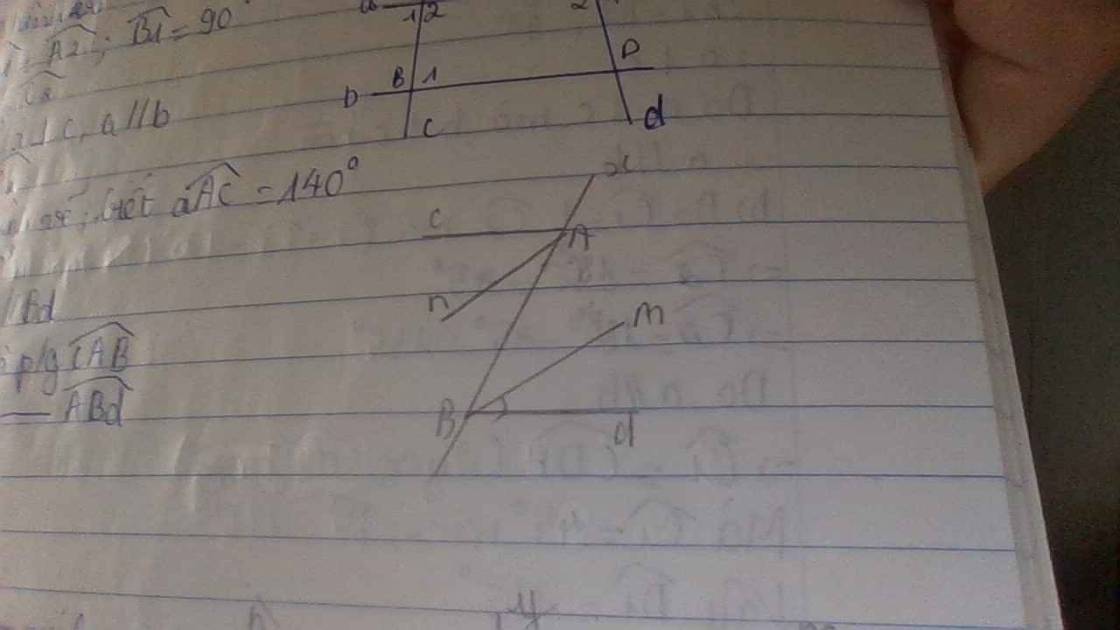
Giúp mình với ạ, chiều nay mình học rùi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

, Tự vẽ hình và ghi giả thiết kết luận (mình không biết vẽ hình trên máy -_-")
Giải : Từ giả thiết ta có
D là trung điểm của AB và MO
,E là trung điểm của AC và ON
=> ED là đường trung bình của cả hai tam giác ABC và OMN
Áp dụng định lý đường trung bình vào tam giác trên ,ta được
\(\hept{\begin{cases}AD//BC,DE//MN\\DE=\frac{1}{2}BC,DE=\frac{1}{2}MN\end{cases}}\Rightarrow\hept{\begin{cases}MN//BC\\MN=BC\end{cases}}\)
Tứ giác MNCB có hai cạnh đối song song và bằng nhau nên nó là hình bình hành
Từ từ ,hình như mình làm nhầm đề :) Để mình làm lại đã rồi trả lời bn sau nhé!!!!!@@

a: \(\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-40^0}{2}=70^0\)
Ta có: ΔABC cân tại A
mà AH là đường trung tuyến
nên AH là đường cao
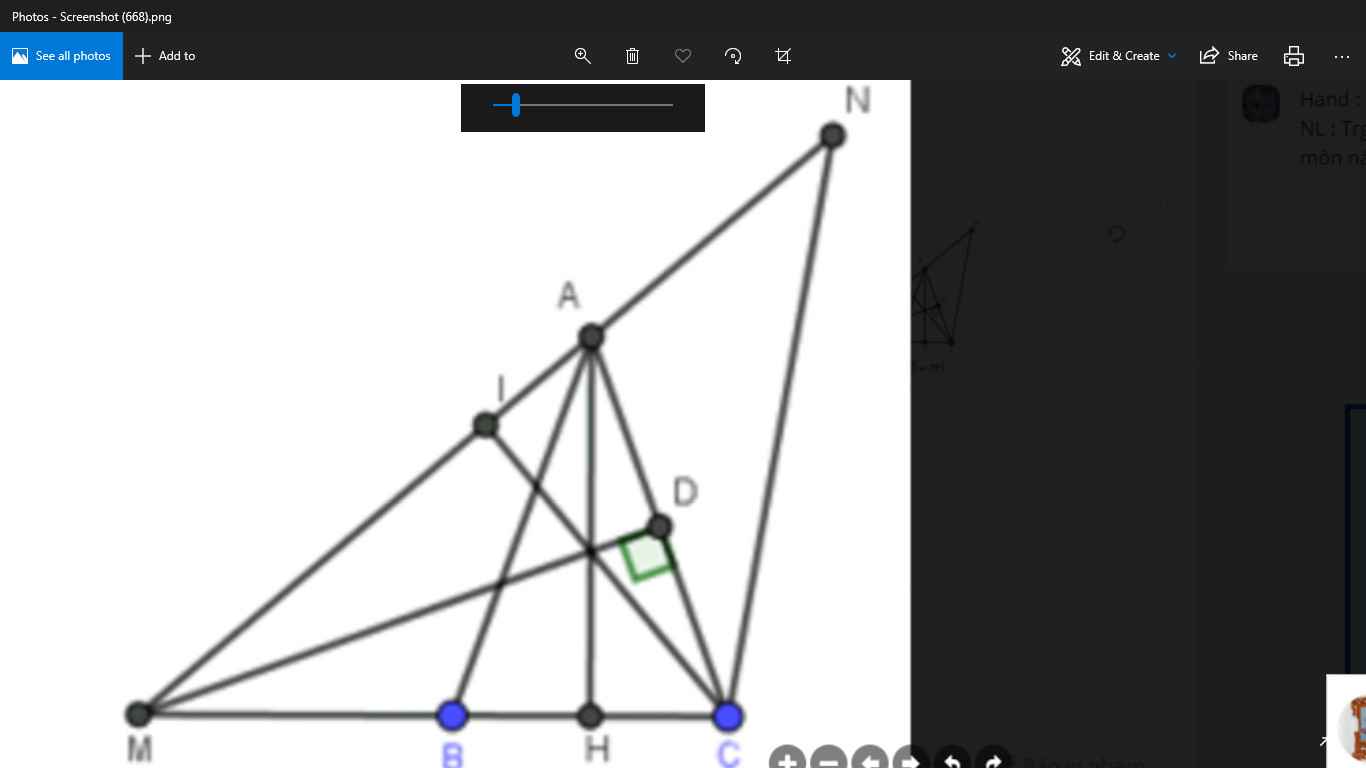
\(\text{a)}\Delta ABC\text{ cân tại }A\text{ có }\widehat{A}=40^0\)
\(\Rightarrow\widehat{ABC}=\widehat{ACB}=\dfrac{180^0-40^0}{2}=70^0\)
\(\text{Xét }\Delta ABH\text{ và }\Delta ACH\text{ có:}\)
\(AB=AC\left(gt\right)\)
\(\widehat{ABC}=\widehat{ACB}\left(cmt\right)\)
\(BH=CH\text{(H là trung điểm BC)}\)
\(\Rightarrow\Delta ABH=\Delta ACH\left(c.g.c\right)\)
\(\Rightarrow\widehat{ÂHB}=\widehat{AHC}\)
\(\text{mà }\widehat{AHB}+\widehat{AHC}=180^0\)
\(\Rightarrow\widehat{AHB}=\widehat{AHC}=90^0\)
\(\Rightarrow AH\perp BC\)
\(\text{b)}\Delta AMC\text{ cân tại M}\text{ vì MD là đường trung trực}\)
\(\Rightarrow\widehat{MAD}=\widehat{MCD}=70^0\)
\(\text{Ta có:}\widehat{MAD}=\widehat{MAH}+\widehat{CAH}\)
\(\Rightarrow\widehat{MAH}=\widehat{MAD}-\widehat{CAH}=70^0-\dfrac{40^0}{2}=50^0\text{(vì AH là phân giác }\widehat{BAC}\text{)}\)
\(\text{c)Xét }\Delta ABM\text{ và }\Delta CAN\text{ có:}\)
\(BM=AN\text{(cách lấy điểm N)}\)
\(AB=AC\left(cmt\right)\)
\(\widehat{ABM}=\widehat{CAN}=180^0-70^0=110^0\)
\(\Rightarrow\Delta ABM=\Delta CAN\left(c.g.c\right)\)
\(\Rightarrow AM=AN\text{(hai cạnh tương ứng)}\)
\(\text{d)Xét }\Delta MIC\text{ và }\Delta NIC\text{ có:}\)
\(IC\text{ cạnh chung}\)
\(\widehat{MIC}=\widehat{NIC}=90^0\)
\(\widehat{IMC}=\widehat{INC}\text{(vì }\Delta ABM=\Delta CAN\text{)}\)
\(\Rightarrow\Delta MIC=\Delta NIC\left(gn.cgv\right)\)
\(\Rightarrow MI=NI\)
\(\Rightarrow\text{I là trung điểm MN}\)
a) Để chứng minh rằng Ac//Bd, ta cần chứng minh rằng tổng các góc nội tiếp trên cung cùng phía của đường tròn đều bằng 180 độ. Vì góc aAc = 140 độ và góc ABd = 40 độ, nên tổng các góc nội tiếp trên cung cùng phía của đường tròn là 140 độ + 40 độ = 180 độ. Do đó, ta có Ac//Bd.
b) Để chứng minh rằng Am là phân giác góc cABG, ta cần chứng minh rằng góc cAmB = góc cABG. Vì góc cAmB là góc nội tiếp trên cung cùng phía với góc cABG, nên góc cAmB = (180 độ - góc cABG) / 2 = (180 độ - 140 độ) / 2 = 40 độ. Vậy, Am là phân giác góc cABG.
c) Để chứng minh rằng An//Bm, ta cần chứng minh rằng tổng các góc nội tiếp trên cung cùng phía của đường tròn là 180 độ. Vì góc cAmB = 40 độ và góc ABd = 40 độ, nên tổng các góc nội tiếp trên cung cùng phía của đường tròn là 40 độ + 40 độ = 80 độ. Do đó, ta không thể kết luận rằng An//Bm.
khó quaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaaas