Cho A= Sin4α(1+2Cos2α)+Cos4α(1+2Sin2α)
Rút gọn A
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H
25 tháng 6 2023
\(a,cos^4a-sin^4a=2cos^2a-1\\ VT=\left(cos^2a-sin^2a\right)\left(cos^2a+sin^2a\right)\\ =cos^2a-sin^2a\\ =cos2a=2cos^2a-1\)
\(b,VT=\dfrac{cos^2a+\dfrac{sin^2a}{cos^2a}-1}{sin^2a}\\ =\dfrac{\dfrac{cos^4a+sin^2a-cos^2a}{cos^2a}}{sin^2a}\\ =\dfrac{\dfrac{cos^4a+\left(1-cos^2a\right)-cos^2a}{cos^2a}}{sin^2a}\\ =\dfrac{\dfrac{cos^4a+1-2cos^2a}{cos^2a}}{sin^2a}\\ =\dfrac{\dfrac{\left(1-cos^2a\right)^2}{cos^2a}}{sin^2a}\\ =\dfrac{sin^4a}{cos^2a}:sin^2a\\ =\dfrac{sin^4a}{cos^2a}\times\dfrac{1}{sin^2a}\\ =\dfrac{sin^2a}{cos^2a}=tan^2a\)
CM
22 tháng 11 2019
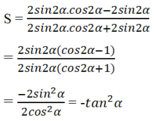
Đáp án: A
Ta cũng có thể suy luận cos2α – 1 < 0, cos2α + 1 > 0 nên S < 0, do đó các phương án B, C, D bị loại. Vậy đáp án là A.
25 tháng 7 2023
a: (sina+cosa)^2
=sin^2a+cos^2a+2*sina*cosa
=1+sin2a
b: \(cos^4a-sin^4a=\left(cos^2a-sin^2a\right)\left(cos^2a+sin^2a\right)\)
\(=cos^2a-sin^2a=cos2a\)
CH
17 tháng 8 2021
\(\left(sin^2\alpha\right)^2+\left(cos^2\alpha\right)^2+2.sin\alpha.cos\alpha\\ =\left(sin^2\alpha+cos^2\alpha\right)^2\\ =\left(1\right)^2=1\)
\(A=sin^4a+2\cdot sin^4a\cdot cos^2a+cos^4a+2\cdot cos^4a\cdot sin^2a\)
\(=\left(sin^4a+cos^4a\right)+2\cdot sina^2a\cdot cos^2a\left(sin^2a+cos^2a\right)\)
\(=sin^4a+cos^4a+2\cdot sin^2a\cdot cos^2a\)
\(=\left(sin^2a+cos^2a\right)^2=1\)