 bài 4 thôi
bài 4 thôi
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


4:
\(A=\left(6\cdot\dfrac{5}{3}-\dfrac{7}{6}\cdot\dfrac{6}{7}\right):\left(\dfrac{21}{5}\cdot\dfrac{10}{11}+\dfrac{57}{11}\right)\)
\(=\left(10-1\right):\left(\dfrac{42}{11}+\dfrac{57}{11}\right)\)
=9/9=1



4:
1/x+1/y+1/z=0
=>(xy+yz+xz)/xyz=0
=>xy+yz+xz+0
=>yz=-xy-xz
x^2+2yz=x^2+yz-xy-xz
=(x-y)(x-z)
Tương tự, ta sẽ có: y^2+2xz=(y-x)(y-z)
z^2+2xy=(z-x)(z-y)
\(A=\dfrac{yz}{\left(x-y\right)\left(x-z\right)}+\dfrac{xz}{\left(y-x\right)\cdot\left(y-z\right)}+\dfrac{xy}{\left(z-x\right)\left(z-y\right)}\)
\(=\dfrac{yz\left(y-z\right)-xz\left(x-z\right)+xy\left(x-y\right)}{\left(x-y\right)\left(x-z\right)\left(y-z\right)}\)
\(=1\)


b1: vì tam giác ABC cân => AB=AC
Xét tam giác ADB và ADC có:
AD cạnh chung
AB=AC
góc ADB = góc ADC
do đó : tam giác ADB = tam giác ADC ( c-g-c)

4:
c; =>|x-1|+|x+2|=3
TH1: x<-2
Pt sẽ là -x-2+1-x=3
=>-2x-1=3
=>-2x=4
=>x=-2(loại)
TH2: -2<=x<1
Pt sẽ là x+2+1-x=3
=>3=3(luôn đúng)
TH3: x>=1
Pt sẽ là x-1+x+2=3
=>2x-1=3
=>2x=4
=>x=2(nhận)

Bài 1:
\(a,ĐK:x+5\ge0\Leftrightarrow x\ge-5\\ b,ĐK:\dfrac{2021}{4-2x}\ge0\Leftrightarrow4-2x>0\Leftrightarrow x< 2\)
Bài 2:
\(a,=5\sqrt{3}-4\sqrt{3}-10\sqrt{3}-3\sqrt{3}=-12\sqrt{3}\\ b,=2\sqrt{5}+\dfrac{8\left(3-\sqrt{5}\right)}{4}=2\sqrt{5}+6-2\sqrt{5}=6\)
Bài 3:
\(A=\dfrac{\sqrt{x}-2+2\sqrt{x}+4+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{3}{\sqrt{x}-2}\)
Bài 4:
\(a,\Leftrightarrow\left|3x-2\right|=7\Leftrightarrow\left[{}\begin{matrix}3x=9\\3x=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-\dfrac{5}{3}\end{matrix}\right.\\ b,ĐK:x\ge\dfrac{1}{2}\\ PT\Leftrightarrow5\sqrt{2x-1}-\sqrt{2x-1}=12\\ \Leftrightarrow\sqrt{2x-1}=3\Leftrightarrow2x-1=9\\ \Leftrightarrow x=5\left(tm\right)\)
Bài 5:
\(b,\Leftrightarrow\left\{{}\begin{matrix}m-1=2\\2m+\sqrt{5}\ne-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m=3\\m\ne\dfrac{-3-\sqrt{5}}{2}\end{matrix}\right.\Leftrightarrow m=3\)
1,
a, x khác phân số có mẫu là 0
b,x khác 2
4,
a, theo đề:
=>(3x-2)^2=49
=>3x-2=7
x=3
bt cs nhiu đây à :<

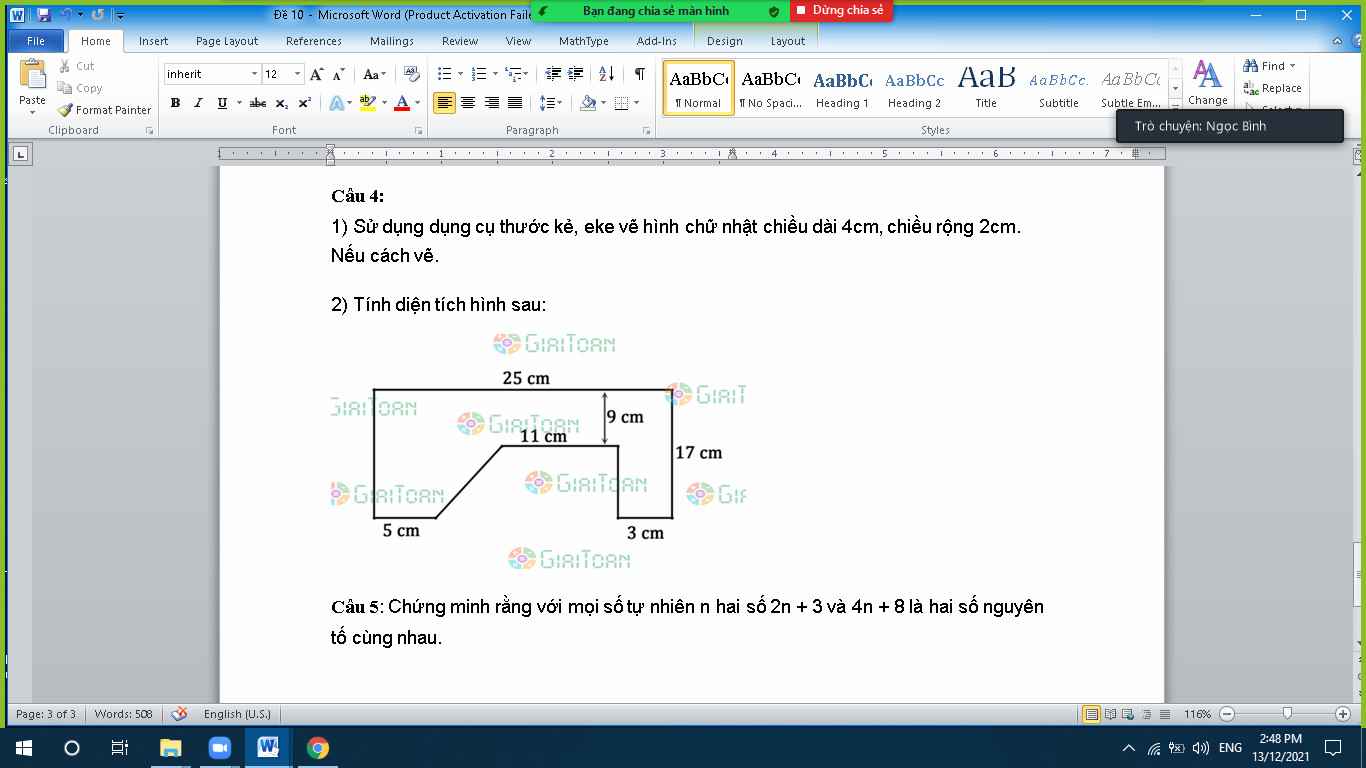


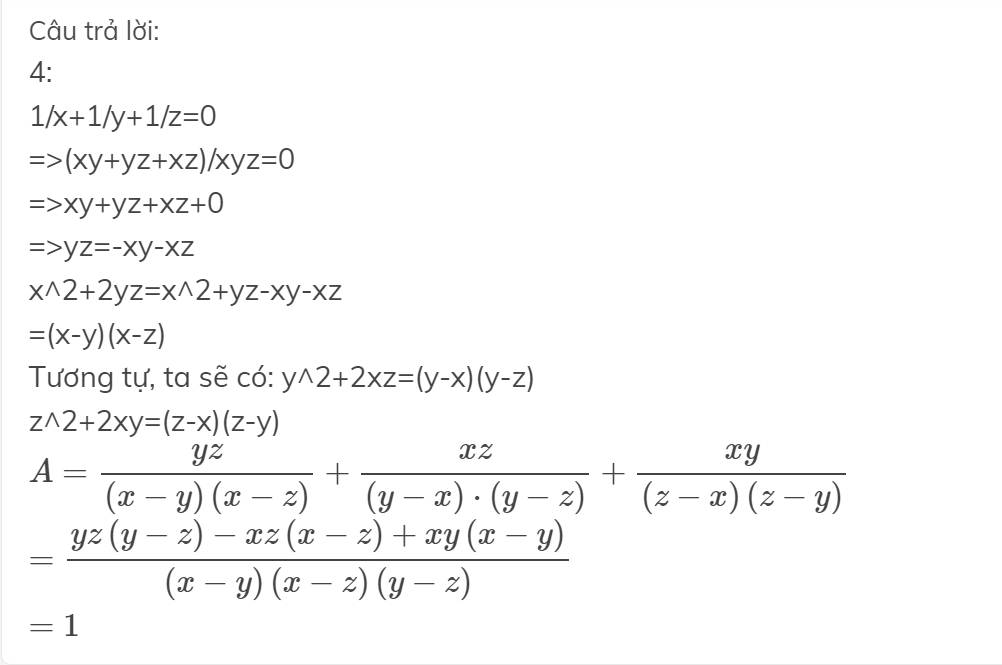


 bài 4 câu c thôi ạ
bài 4 câu c thôi ạ
4:
a: A=|x-7/4|+8/5
|x-7/4|>=0
=>|x-7/4|+8/5>=8/5
Dấu = xảy ra khi x=7/4
b: B=|x-5|+|x+3/4|
=>B=|x+3/4|+|5-x|>=|x+3/4+5-x|=23/4
Dấu = xảy ra khi (x-5)(x+3/4)<=0
=>-3/4<=x<=5
a)\(A=\left|x-\dfrac{7}{4}\right|+1\dfrac{3}{5}\)
\(A=\left|x-\dfrac{7}{4}\right|+\dfrac{8}{5}\)
Mà: \(\left|x-\dfrac{7}{4}\right|\ge0\forall x\) nên
\(\Rightarrow A=\left|x-\dfrac{7}{4}\right|+\dfrac{8}{5}\ge\dfrac{8}{5}\)
Dấu "=" xảy ra:
\(\left|x-\dfrac{7}{4}\right|+\dfrac{8}{5}=\dfrac{8}{5}\)
\(\Rightarrow x=\dfrac{7}{4}\)
Vậy: \(A_{min}=\dfrac{8}{5}\) khi \(x=\dfrac{7}{4}\)
b) \(B=\left|x-5\right|+\left|x+\dfrac{3}{4}\right|\)
Mà: \(B=\left|5-x\right|+\left|x+\dfrac{3}{4}\right|\ge\left|5-x+x+\dfrac{3}{4}\right|=\dfrac{23}{4}\)
Dấu "=" xảy ra:
\(\left(5-x\right)\left(x+\dfrac{3}{4}\right)\le0\)
\(\Rightarrow\left\{{}\begin{matrix}x\le5\\x\ge-\dfrac{3}{4}\end{matrix}\right.\)
\(\Rightarrow-\dfrac{3}{4}\le x\le5\)
Vậy: \(B_{min}=\dfrac{23}{4}\) khi \(-\dfrac{3}{4}\le x\le5\)