cho tam giác ABC vuông tại A, đường cao AH. gọi D là hình chiếu của H trên AC. gọi E là hình chiếu cửa H trên AB. biết HD= 18cm, HE=12cm. tính AB, AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
10 tháng 10 2023
Đúng(0)
Những câu hỏi liên quan
KT
16 tháng 7 2018
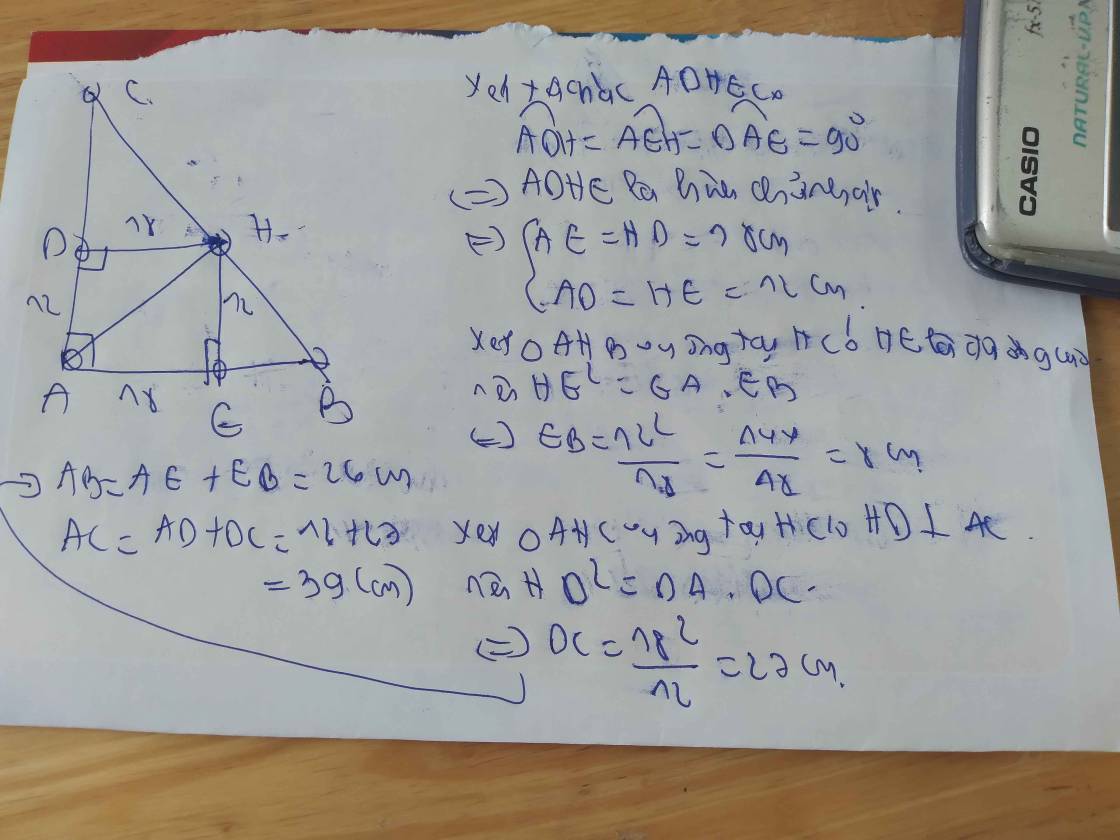
Dễ dàng chứng minh được: \(HEAD\)là hình chữ nhật
\(\Rightarrow\)\(HE=AD=12\)
\(HD=EA=18\)
Áp dụng hệ thức lượng ta có:
\(HD^2=AD.DC\)
\(\Rightarrow\)\(DC=\frac{HD^2}{AD}\)
\(\Rightarrow\)\(DC=\frac{18^2}{12}=27\)
\(\Rightarrow\)\(AC=AD+DC=12+27=39\)
\(HE^2=BE.AE\)
\(\Rightarrow\)\(BE=\frac{HE^2}{AE}\)
\(\Rightarrow\)\(BE=\frac{12^2}{18}=8\)
\(\Rightarrow\)\(AB=BE+EA=8+18=26\)
5 tháng 8 2023
a: BC=BH+CH=25cm
Xét ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC; AC^2=CH*BC; AH^2=HB*HC
\(AB=\sqrt{BH\cdot BC}=\sqrt{9\cdot25}=15\left(cm\right)\)
\(AC=\sqrt{16\cdot25}=20\left(cm\right)\)
\(AH=\sqrt{HB\cdot HC}=12\left(cm\right)\)
b: Xét tứ giác ADHE có
góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
5 tháng 8 2023
a: BC=BH+CH=25cm
Xét ΔABC vuông tại A có AH là đường cao
nên AB^2=BH*BC; AC^2=CH*BC; AH^2=HB*HC
\(AB=\sqrt{BH\cdot BC}=\sqrt{9\cdot25}=15\left(cm\right)\)
\(AC=\sqrt{16\cdot25}=20\left(cm\right)\)
\(AH=\sqrt{HB\cdot HC}=12\left(cm\right)\)
b: Xét tứ giác ADHE có
góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật