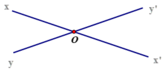
cho 2 đường thẳng xx"và yy" cắt nhauntaij a kể tên các cặp góc đối đỉnh
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
2 tháng 11 2023
a) Các cặp góc kề bù
\(\widehat{xOy}\) và \(\widehat{yOx'}\)
\(\widehat{yOx'}\) và \(\widehat{x'Oy'}\)
\(\widehat{x'Oy'}\) và \(\widehat{xOy'}\)
\(\widehat{xOy'}\) và \(\widehat{xOy}\)
Các cặp góc đối:
\(\widehat{xOy}\) và \(\widehat{x'Oy'}\)
\(\widehat{x'Oy}\) và \(\widehat{y'Ox}\)
b) Do \(\widehat{xOy}\) kề bù với \(\widehat{xOy'}\)
\(\Rightarrow\widehat{xOy}+\widehat{xOy'}=180^o\)
\(\Rightarrow\widehat{xOy'}=180^o-70^o=110^o\)
CM
18 tháng 12 2019
Cặp góc đối đỉnh:
x O y ^ v à x ' O y ' ^ ; x O y ' ^ v à x ' O y ^
24 tháng 10 2021
do x'Ôy' và xÔy là hai cặp góc đối đỉnh nên suy ra x'Ôy' = xÔy (50o)
3 tháng 7 2018
115 o x y y' x' A
a, Các cặp góc đối đỉnh là :
\(\widehat{xAy}\)với\(\widehat{y'Ax'}\)
\(\widehat{xAy'}\)với \(\widehat{yAx'}\)
b, Do \(\widehat{xAy'}\)đối đỉnh với\(\widehat{yAx'}\)
\(=>\)\(\widehat{xAy'}\)\(=\)\(\widehat{yAx'}\)\(=\)\(115^o\)
Lại có \(\widehat{xAy'}\)\(+\)\(\widehat{y'Ax'}\)\(=\)\(180^o\)
\(=>\)\(115^o\)\(+\)\(\widehat{y'Ax'}\)\(=180^o\)
\(=>\)\(\widehat{y'Ax'}\)\(=65^o\)
Mà \(\widehat{xAy}\)đối đỉng với \(\widehat{x'Ay'}\)
\(=>\)\(\widehat{xAy}\)\(=\widehat{x'Ay'}\)=\(65^o\)
Vậy \(\widehat{xAy'}\)\(=\widehat{yAx'}\)\(=150^o\)
\(\widehat{xAy}\)\(=\widehat{x'Ay'}\)\(=65^o\)
Chúc bạn họk tốt ~~~!!:3
Ủng hộ nhé
25 tháng 8 2016
x A x' y y'
Hai cặp góc đối đỉnh là:
- xAy và x'Ay'
- x'Ay và xAy'
^...^ 
^_^
SA
12 tháng 6 2018
Hình vẽ x y z x' y' z' 1 2 3 4 5 6 O
a) Các cặp góc bằng nhau là:
xOx' = yOy' = zOz' = 180o
O1 = O4
O2 = O5
O3 = O6
xOz = x'Oz'
yOx' = y'Ox
b) Góc đối đỉnh xOz là x'Oz'
Góc đối đỉnh yOx' là x'Oz'
c) - Ta có: xOy + x'Oy = 180o ( hai góc kề bù )
=> 50o + x'Oy = 180o
=> x'Oy = 180o - 50o
=> x'Oy = 130o
- Ta có: x'Oy = xOy' = 130o ( hai góc đối đỉnh )
Vậy x'Oy = 130o
xOy' = 130o
x x' y y' a
Các cặp góc đối đỉnh là :góc XAY đối đỉnh với góc X'AY'
góc XAY' đối đỉnh với góc X'AY
lam theo vu thi hoa di dung roi do