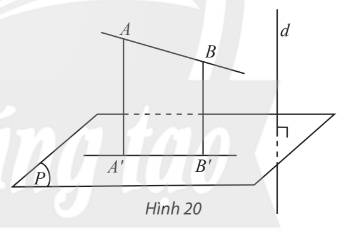
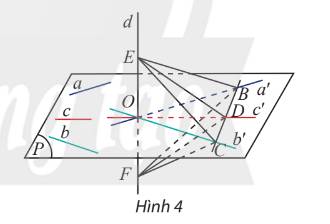
a) Cho đường thẳng \(a\) song song với mặt phẳng \(\left( P \right)\). Lấy hai điểm \(A,B\) tuỳ ý trên \(a\) và gọi \(H,K\) lần lượt là hình chiếu vuông góc của \(A\) và \(B\) trên \(\left( P \right)\) (Hình 4a). So sánh độ dài hai đoạn thẳng \(AH\) và \(BK\).
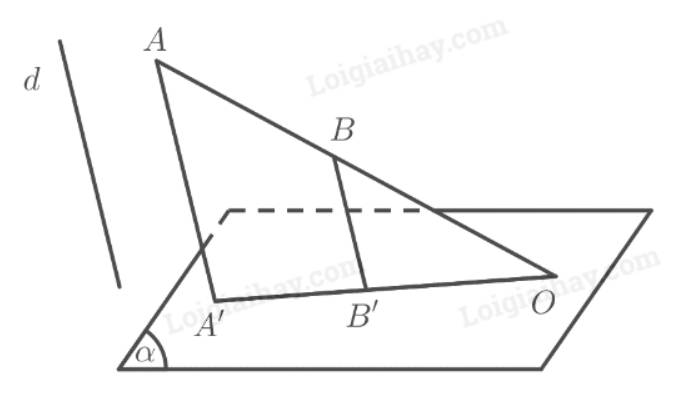
b) Cho hai mặt phẳng song song \(\left( P \right)\) và \(\left( Q \right)\). Lấy hai điểm \(A,B\) tuỳ ý trên \(\left( P \right)\) và gọi \(H,K\) lần lượt là hình chiếu vuông góc của \(A\) và \(B\) trên \(\left( Q \right)\) (Hình 4b). So sánh độ dài hai đoạn thẳng \(AH\) và \(BK\).



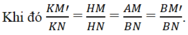
a) Ta có:
\(\left. \begin{array}{l}AH \bot \left( P \right)\\BK \bot \left( P \right)\end{array} \right\} \Rightarrow AH\parallel BK\)
Mà \(AB\parallel HK\)
\( \Rightarrow ABKH\) là hình bình hành có \(AH \bot \left( P \right) \Rightarrow AH \bot HK \Rightarrow \widehat {AHK} = {90^ \circ }\)
Vậy \(ABKH\) là hình chữ nhật.
Vậy \(AH = BK\).
b) Ta có:
\(\left. \begin{array}{l}AH \bot \left( Q \right)\\BK \bot \left( Q \right)\end{array} \right\} \Rightarrow AH\parallel BK\)
Mà \(AB\parallel HK\)
\( \Rightarrow ABKH\) là hình bình hành có \(AH \bot \left( Q \right) \Rightarrow AH \bot HK \Rightarrow \widehat {AHK} = {90^ \circ }\)
Vậy \(ABKH\) là hình chữ nhật.
Vậy \(AH = BK\).